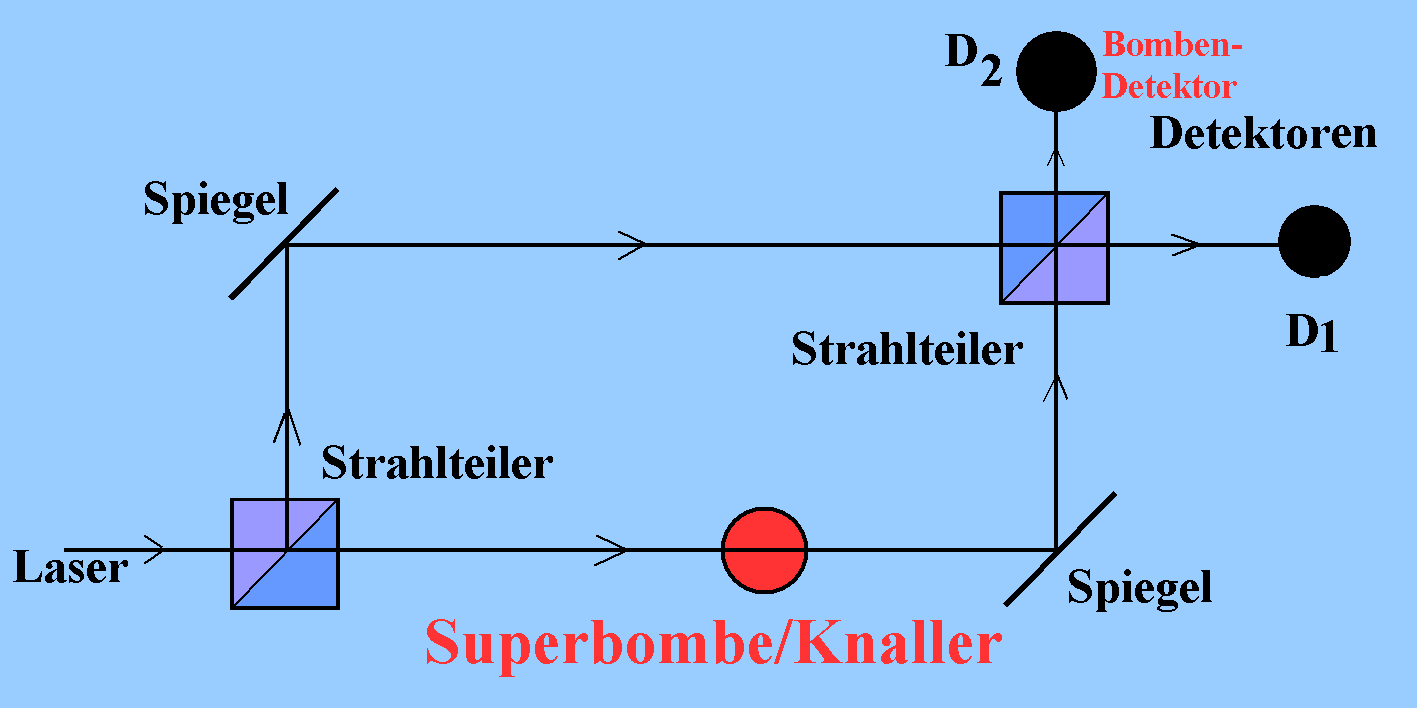
(1) Bei einem Mach-Zehnder- Interferometer ist es sinnlos, vom Weg eines Photons zu sprechen, wenn ein solcher nicht gemessen wird. Deswegen kommt im Normalfall Interferenz zustande, weil zwischen den zwei klassisch denkbaren Möglichkeiten des Wegs nicht unterschieden wird. Es lässt sich einrichten, dass D1 bei jedem Photon anspricht, D2 nie. (2) Stellt man aber ein Hindernis in einen Interferometer-Arm des Interferometers, z.B. den unteren, findet weder für D1 noch für D2 eine Interferenz von zwei Möglichkeiten statt: Beide Detektoren sprechen in jeweils 25% aller Fälle an. In den anderen 50% der Fälle blockiert das Hindernis die Photonen. D1 spricht an, wenn Licht am linken Strahlteiler nach oben gelenkt wird (in 50% aller Fälle) und dann (in 50% dieser Fälle) am rechten Strahlteiler geradeaus passiert, also in insgesamt 25% aller Fälle. D2 spricht an, wenn Licht am linken Strahlteiler ebenfalls nach oben gelenkt wird (in 50% aller Fälle) und dann (in 50% dieser Fälle) am rechten Strahlteiler noch einmal reflektiert wird, also in insgesamt 25% aller Fälle. Die übrigen 50% aller einfallenden Photonen werden vom Hindernis absorbiert oder verlassen dort sonstwie das Interferometer. Ersetzt man das Hindernis durch einen Detektor, dann kann man dies als Gewinnung einer WWI auffassen, auch dann, wenn der Detektor Photonen messen könnte ohne sie zu vernichten. Auch in diesem Fall würde die Interferenz verschwinden. Beide Detektoren D1 und D2 würden bei langer Versuchsdauer im Mittel gleich viele Photonen registrieren.

(3) Besonders drastisch wurde der Versuch von Elitzur und Vaidman (1993) vorgeschlagen: Das Hindernis soll eine Superbombe sein, die sich aber einer Entschärfung dadurch widersetzt, dass bereits ein einziges Photon genügt, um sie zur Explosion zu bringen. Es musste also etwas gefunden werden, mit dem man die Anwesenheit der Bombe erkennt, "ohne hinzuschauen". In 25 % der Fälle spricht der Detektor D2 ("Bombendetektor") an und verrät so die Anwesenheit der Bombe ohne dass sie hochgeht. Allerdings, in 50 % der Fälle wird sie explodieren. Detektor D1 spricht in 25 % der Fälle an, obwohl eine Bombe vorhanden ist. Sein Ansprechen besagt also in diesem Fall gar nichts. In einer wieder entschärften Version heißt dieser Versuch oft "Knaller-Test", weil die Superbombe durch einen einfachen Knaller ersetzt ist. (4) Von einem Weg des Photons zu sprechen hat in diesem Fall nur dann einen Sinn, wenn die Bombe hochgeht (dann weiß man, dass das Photon den unteren Weg gewählt hat) oder wenn trotz Anwesenheit der Bombe einer der Detektoren anspricht und die Bombe nicht hochgeht (dann weiß man, dass das Photon den hindernisfreien oberen Weg gewählt hat). Ist unbekannt, ob eine Bombe vorhanden ist, und D1 spricht an, könnte das an der Interferenz liegen. Dann passt das Bild, dass das Photon einen be-stimmten Weg gewählt hat, gar nicht.

(5) Wie Kwiat, Weinfurter und Zeilinger gezeigt haben, lässt sich die Anordnung so modifizieren, dass die Bombe praktisch nie hochgeht und trotzdem praktisch immer ohne "gesehen" zu werden entdeckt wird. Sie benutzten dazu den so genannten Quanten-Zeno-Effekt. (6) Die Tatsache, dass D2 in 25% der Fälle anspricht, obwohl eine Bombe vorhanden ist, die nicht hochgeht, formulieren manche Physiker in ihrem Jargon so als "schaue das nachgewiesene Photon erst nach, ob der 'Bombenweg' offen oder gesperrt ist, bevor es den anderen Weg  bis zu D2 geht", den Detektor D2 zum Ansprechen bringt und so die Existenz einer Bombe meldet. Das darf man nicht wörtlich auffassen!

E

1. Raffinierte Anwendung zur Demonstration, dass es im Mach-Zehnder-Interferometer ebenso wie beim Doppelspalt-Versuch keinen Weg der Teilchen in ihm ohne eine Messung gibt. Das Hindernis stellt eine solche Messung dar, die die Interferenz verschwinden lässt. 2. Der Versuch erläutert auch die Tatsache, dass die Interferenz bereits dann verloren geht, wenn nur die Möglichkeit zu einer Wegmessung besteht, sie nur "angedroht wird", aber tatsächlich nicht durchgeführt wird (das Photon trifft mit einer beträchtlichen Wahrscheinlichkeit gar nicht die Superbombe, obwohl sie vorhanden ist).