Beim Fotoeffekt "schlagen" Photonen mit der Energie Eph
aus der Fotokathode Fotoelektronen heraus, indem sie die Austrittsarbeit
Wo verrichten und den Rest den Elektronen als kinetische
Energie Ekin mitgeben. Mit der Fotozelle misst du angeblich
die kinetische Energie Ekin der schnellsten Fotoelektronen,
nachdem sie beim Austritt aus der Fotokathode eine bestimmte
Austrittsarbeit Wo verrichtet haben. Ekin = Eph
- Wo wird mit der Gegenspannungsmethode oder der Auflademethode
gemessen. Die Gegenspannung oder Bremsspannung wird soweit erhöht, bis
die "schnellsten Photoelektronen gerade nicht mehr gegen die
Bremsspannung anlaufen können". Bei dieser Spannung UB verschwindet
der Photostrom I gerade. Ihre kinetische Energie ist dann in die
potenzielle Energie e·UB umgewandelt worden.
|
|
Leider gibt es hier ein Problem: Genau genommen
gibt es diese "schnellsten Fotoelektronen" bei Raumtemperatur
nicht, wo du doch den Versuch durchführst. Bedingt durch die
festkörperphysikalischen Eigenheiten der Metallkathode können
die austretenden Fotoelektronen zusätzliche kinetische Energien
erhalten, die stark streuen, aber doch meistens in einem Bereich
der Breite kB·T, wobei T die absolute Temperatur und
kB die Boltzmann-Konstante ist. Statt von der
kinetische Energie Ekin "der schnellsten
Fotoelektronen" müsste man eigentlich von der kinetische Energie
Ekin "der am absoluten Temperaturnullpunkt ( T = 0 )
schnellsten Fotoelektronen" sprechen.
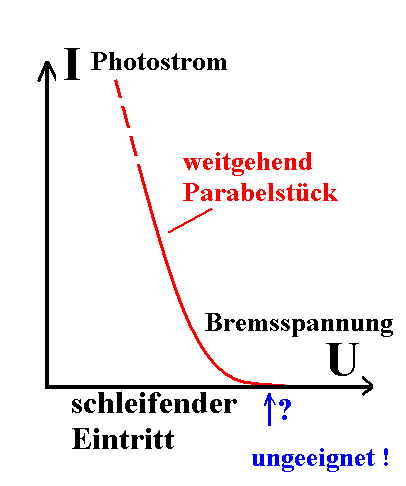
Eine Folge dieser Problematik ist es, dass rein
technisch diese Energie normalerweise nicht frei von Willkür zu
bestimmen ist. Du hast vielleicht von dem "schleifenden
Eintritt" der U-I-Kurve gehört (links; schematisch für eine
bestimmte Lichtfrequenz).
|
Wie sollte man die kinetische Energie Ekin "der
am absoluten Temperaturnullpunkt ( T = 0 ) schnellsten Fotoelektronen"
messen? Herunterkühlen der Fotozelle auf T = 0 kommt wohl nicht in
Frage.
Also, wie kann man bei endlichen Temperaturen die
kinetische Energie Ekin "der am absoluten Temperaturnullpunkt
( T = 0 ) schnellsten Fotoelektronen" bestimmen? Die Theorie
des
Fotoeffekts bei einer ebenen Fotokathode zeigt, dass abgesehen von
den erwähnten Temperatureffekten das U-I-Diagramm im wesentlichen eine
Funktion sein sollte, die prop. zu (Eph-W0 - e·U)2
bzw. (Ekin - e·U)2 ist (dieser Ausdruck
berücksichtigt den "schrägen Austritt der Fotoelektronen aus der
Fotokathode"). Wenn e·U deutlich von Ekin = Eph -
Wo abweicht (Eph
Photonenenergie, Wo Austrittsarbeit), spielen Energien in der
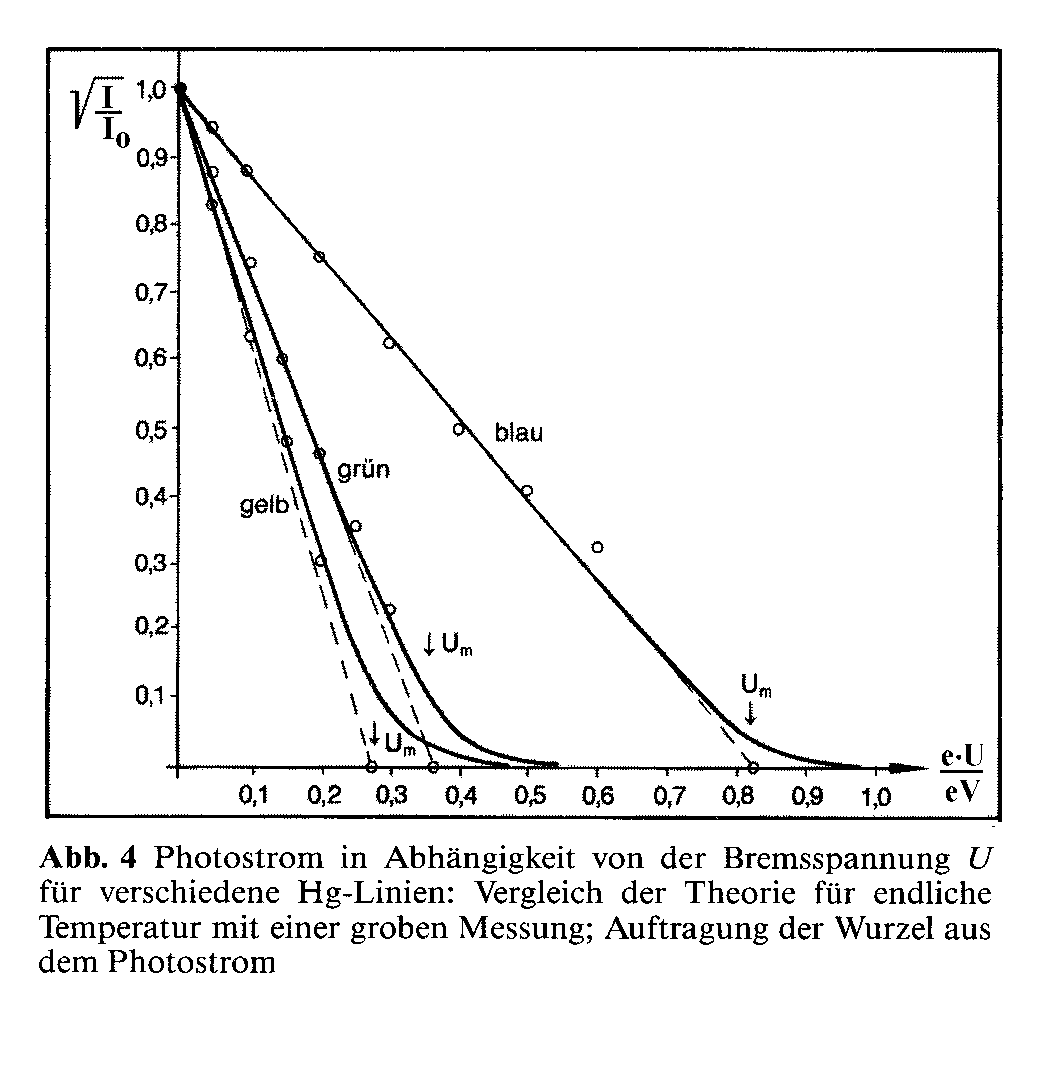
Größenordnung von kB·T keine Rolle mehr. Trägt man also √I
gegenüber e·U auf, dann wird man bemerken, dass √I nie 0 wird
(Bestätigung der Tatsache, dass es die schnellsten Fotoelektronen nicht
gibt). Aber, der U-√I-Graph ist in weiten Bereichen ein Geradenstück,
das eine leichte Extrapolation ermöglicht. Wenn man von höheren Strömen
I her extrapoliert, findet man eine scheinbare Nullstelle von I, die den
Temperatureffekt nicht berücksichtigt, die eine echte Nullstelle wäre,
wenn T = 0.
|
|
Du gehst also so vor (Wurzelmethode):
Miss I und U bei Werten von e·U > kB·T
(bei sehr hohen Spannungen kommen andere Effekte hinzu, aber
wenige Zehntel eV oberhalb der erwarteten Ekin der
Fotoelektronen kannst du nichts falsch machen). Trage √I
[normiert auf den Maximalwert I0, also √(I/I0)]
gegenüber e·U auf. Es wird sich weitgehend eine Gerade ergeben
mit Abweichungen bei kleinen Strömen. Verlängere die Gerade bis
I = 0. Dort liest du das gesuchte e·U bzw. Ekin ab
(in der Abb. als Um bezeichnet).
(Abbildung links nach H. Hübel, Über den
Photoeffekt in der Schule - Vergleich mit einem
festkörperphysikalischen Modell, Praxis der Naturwissenschaften,
Teil Physik, 36 (1987), Heft 6, S. 39)
|
Diese Methode ist frei von Willkür und liefert erstaunlich
gute Werte. Im Praktikum einer Universität wurde nach meiner Anregung
hin verfahren und h bis auf 0,5 % erhalten (vgl. sonstige Fehlerquellen)!
.
Bei der Auflademethode entsteht das gleiche
Problem; im Prinzip gibt es Fotoelektronen mit weitgehend beliebiger
Energie, die den Kondensator bis zu weitgehend beliebigen Spannungen
aufladen müssten, wenn nicht ... ? Ja, wenn nicht der endliche
Isolationswiderstand der Fotozelle das verhindern würde. Das führt zu
einem weiteren Problem: danach hängt die sich einstellende
Aufladespannung also von zwei Größen ab: Von der kinetischen Energie der
Fotoelektronen und vom Isolationswiderstand. Offenbar schaffen es die
Lehrmittelfirmen, einen Isolationswiderstand zu produzieren, der dieses
Problem nicht in Erscheinung treten lässt.
[1] H. Hübel, Über den Photoeffekt in der Schule -
Vergleich mit einem festkörperphysikalischen Modell, Praxis der
Naturwissenschaften, Teil Physik, 36 (1987), Heft 6, S. 39
[2] H. Hübel: Über
den
Photoeffekt in Schule und Praktikum - die Wurzelmethode
Ungenauigkeiten für h ergeben sich
häufig wegen Streulicht, durch Ausglühen geschädigter Photozelle,
nicht exakt einfarbigem Licht, einem Netzbrumm infolge schlechter
Abschirmung.

