Überlege dir, was bei jeder der zwei Schalterstellungen passiert!
Links ist ein Auflageblatt für den Schülerversuch zur Leybold-Rastersteckplatte abgebildet.
|
SG114 Ein-/Ausschaltvorgänge beim Kondensator ©
H. Hübel Würzburg 2013
|
Impres-sum |
Vgl. bzgl. weiterer Informationen:
|
|
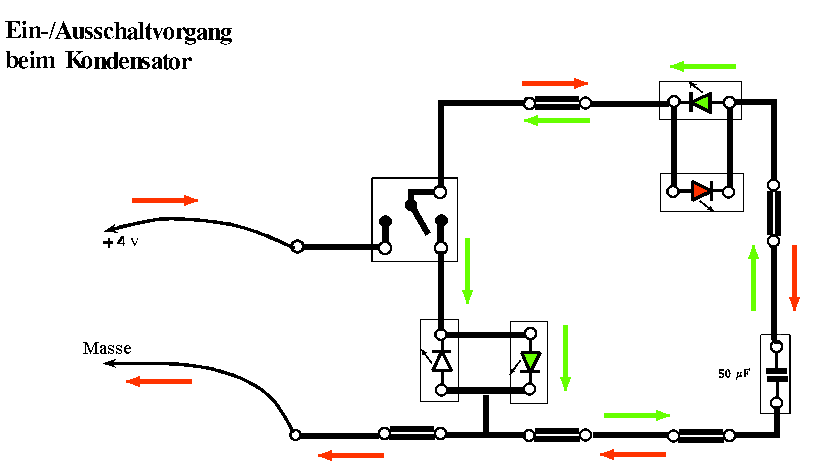
Es soll ein Kondensator geladen und entladen werden. Studiere zuerst mit einer Schülerversuchs-Anordnung die jeweilige Stromrichtung:
 |
Abb. 1: Die Stromrichtung wird jeweils
durch Leuchtdioden (LEDs) angezeigt. Durch eine LED fließt der
Strom nur in Pfeilrichtung. Überlege dir, was bei jeder der zwei Schalterstellungen passiert! Links ist ein Auflageblatt für den Schülerversuch zur Leybold-Rastersteckplatte abgebildet. |
|
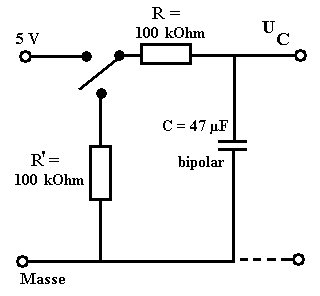
Abb. 2: Schaltung zur quantitativen
Untersuchung von Ein-/Ausschaltvorgängen beim Kondensator -
Messung der Kondensatorspannung UC, z.B. mit einem
Messinterface.
R' kann auch durch einen guten Leiter ersetzt werden. |
Schließt man in der Schaltung nach Abb. 2 den Schalter, so steigt die Spannung erst allmählich an. Umgekehrt, öffnet man den Schalter nach langer Zeit wieder, so klingt der Spannung erst allmählich ab.
Die Vorgänge bei einem Kondensator werden in der Schule
durch drei didaktisch wichtige Bedingungen dominiert. Die vierte
Bedingung ist eine Folgerung:
|
Kondensator
|
|
|
"Grundgesetz des
Kondensators" (1)
|
Q = C·UC bzw. I = - C·dUC/dt, (da I = -dQ/dt, wenn Q die noch auf dem Kondensator vorhandene Ladung und nicht die transportierte ist; UC ist dann die am Kondensator vorhandene Spannung, gegen die die Batterie arbeiten muss, entsprechend einem Spannungsabfall) |
|
Spannungsbilanz (2)
|
UB = I · Rges + UC
(beim Einschalten) bzw. 0 = I · Rges' + UC (beim
Ausschalten) Rges und Rges' sind die
jeweiligen, vom Strom I durchflossenen Gesamtwiderstände (in
Abb. 2 also R bzw. R + R'). |
|
Stetigkeitsbedingung für
die Spannung (3)
|
Die Spannung macht beim Kondensator keine
Sprünge. |
|
Stationäre Spannung
|
Das ist die Spannung, die sich einstellt, wenn der Ladevorgang beendet ist, also, wenn I = 0, also UC = UB ; entsprechend für den Entladevorgang (UC = 0). |
Die Stetigkeitsbedingung hängt mit der Anfangsbedingung
UC(t=0) beim Schalten zusammen. Sie bestimmt auch die Spitzenstromstärken,
wenn noch UC = 0, bzw. wenn noch UC = UB:
| Es muss ein solcher Strom fließen, dass UC kurzzeitig unverändert bleibt. |
Die Differentialgleichung 1. Ordnung für die Kondensator-Spannung benötigt nur eine Anfangsbedingung, hier für die Spannung.
dUC/dt kann je nach Situation oder
Kenntnisstand aufgefasst werden als Zeitableitung der Spannung oder
als Differenzenquotient ΔUC/Δt .
Beispiele für einfache Rechnungen:
Es sollen die Daten von Abb. 2 gelten. Unmittelbar nach Schließen des Schalters ist die Kondensatorspannung noch UC = 0. Nach der Spannungsbilanz fließt also ein unbehinderter Spitzenstrom I = UB / Rges = 5,0 V / 100 kOhm = 50 µA.
Unmittelbar nach dem Öffnen des Schalters entlädt sich der Kondensator über zwei 100 kOhm-Widerstände, UB = 0. Wenn der Kondensator zuvor voll geladen ist: UC = UB = 5,0 V ("Sättigungsspannung"). Nach der Spannungsbilanz (2) folgt der Spitzenstrom I = - UC / Rges' = - 5,0 V / 200 kOhm = - 25 µA. Beide Spitzenströme haben umgekehrtes Vorzeichen, weil es sich einmal um einen Ladestrom handelt, das andere Mal um einen Entladestrom.
.
( Juni 2014 )