Für Schüler ungeeignet:

Die mathematische Aussage der Maxwell-Gleichung div B = 0 wird aufgefasst als mathematische Beschreibung der Beobachtung "Es gibt keine magnetischen Ladungen". Wenn man eine magnetische Ladung entdecken würde, müsste die Maxwell-Gleichung geändert werden. Üblicherweise wird daraus geschlossen, dass (a) magnetische Feldlinien weder Anfang noch Ende haben, und dass sie (b) ringförmig geschlossen seien. In den Situationen der Schulphysik ist beides immer auch experimentell belegt. Eine Feldlinie ist eine gedachte Linie, deren Tangente in jedem ihrer Punkte die Richtung des Felds anzeigt. Ohne Feld kann es also keine Feldlinie geben.

(b) wird in der Regel als Folge von (a) angesehen.

Ich möchte hier darlegen, dass der Schluss von (a) auf (b) voreilig ist. In der Hochschul-Mathematik lernt der Student eine so genannte Peano-Kurve kennen, die er oft nur als eine mathematische Spitzfindigkeit auffasst. Wenn man, an irgendeinem Punkt startend, ihr entlang läuft, kommt man niemals zum Ausgangspunkt zurück. Vielmehr durchläuft man nach und nach alle Punkte des Raums (oder eines Teilraums), aber niemals einen Punkt, an dem man schon einmal gewesen ist. Wenn man das im Gedächtnis hat, ist eine weitere - wenn auch kuriose - Möglichkeit für Feldlinien denkbar.

Seit ca. 100 Jahren wurden solche Überlegungen für eine magnetische Feldlinie angestellt. Diese Feldlinie hat dann weder Anfang noch Ende, ist aber nicht geschlossen: schwer vorstellbar, aber wahr. Wenn man ihr entlang läuft, kommt man nie mehr zum Ausgangspunkt zurück. Künftige mögliche Fusionsreaktoren, speziell Tokomaks, nutzen Magnetfelder, um extrem heiße Gase mit elektrisch geladenen Teilchen von den ringförmigen Gefäßwänden fernzuhalten. Man fand für sie in den letzten Jahrzehnten Feldkonfigurationen, bei denen Felder mit genau solchen Feldlinien ohne Anfang und Ende eine große Rolle spielen. Sie sind zwar kurios, aber offenbar sogar für Anwendungssituationen wichtig.

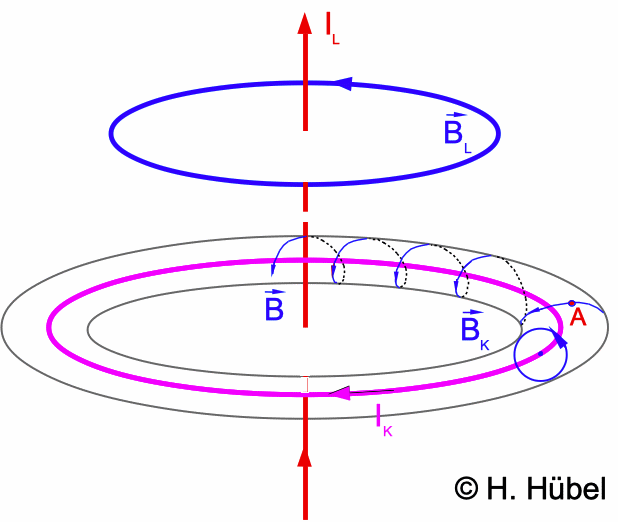
Abb. 1: Feldlinien ohne Anfang und Ende, aber nicht unbedingt geschlossen: Ein Kreisstrom (IK; purpur) allein umgibt sich mit einem Magnetfeld aus ringförmig geschlossenen Feldlinien (BK; blau), die den Strom jeweils umschließen. Für eine bestimmte Feldstärke bilden sie insgesamt einen Torus (schwarz; unten), der den Strom umschließt.

Zu Abb. 1: Ergänzt man nun einen geradlinigen Strom längs der Kreisachse (I_L; rot), so überlagern sich beide Magnetfelder (blau; B_L oben  und B_K unten) mit dem Ergebnis B. Eine Folge ist, dass jetzt die ringförmigen Feldlinien quasi kontinuierlich weiter um den Torus herum transportiert werden. Sie umgeben dann den Torus auf Spiralen. Theoretische Überlegungen und Rechnungen, die auf den russischen Physiker Tamm zurückgehen, zeigen, dass ein Ausgangspunkt A auf dem Torus nie mehr erreicht wird, dass die Feldlinie also endlos um den Torus herum spiralförmig weiter läuft. Zweitens ergeben die Rechnungen, dass das System chaotisch wird. Zwei benachbarte Punkte auf zunächst benachbarten Feldlinien führen dann nicht - wie bei nichtchaotischen Systemen - zu weiterhin benachbart bleibenden Feldlinien, sondern zu Feldlinien, die sich schnell immer weiter voneinander entfernen.

Die Zeichnung in Abb. 1 ist sehr schematisch und soll das Entstehen der Feldlinie ohne Anfang und Ende plausibel machen. Der mathematisch ermittelte tatsächliche Verlauf der Feldlinien weicht davon ab.

Im Zusammenhang mit der Frage, ob wirklich keine magnetische Feldlinie einen Anfang und ein Ende hat, wird auch ein Fall diskutiert, der sich sogar in der Schule mit zwei gegeneinander gerichteten Stabmagneten oder zwei entsprechend orientierten Helmholtz-Spulen realisieren lässt. Die magnetischen Feldlinien laufen in einem bestimmten Bereich aufeinander zu und biegen dann (fast) immer voreinander ab, um zu ihrem jeweiligen S-Pol zurückzukehren. Vielleicht haben Sie sich auch schon gefragt: Was geschieht mit den Feldlinien, die genau auf der Symmetrieachse aufeinander zulaufen? Sie scheinen sich in einem Punkt zu treffen, einem so genannten singulären Punkt. Bei umgekehrter Polung laufen die Feldlinien vom singulären Punkt weg. Wenn man berücksichtigt, wie sich die beiden Felder in der zur Symmetrieachse senkrechten Symmetrieebene vektoriell überlagern, sieht man in ihr Bündel von Feldlinien (mit entgegengesetzten Paaren), die vom singulären Punkt wegstreben bzw. zu ihm hinstreben. Ich nenne alle solchen Feldlinien singuläre Feldlinien.

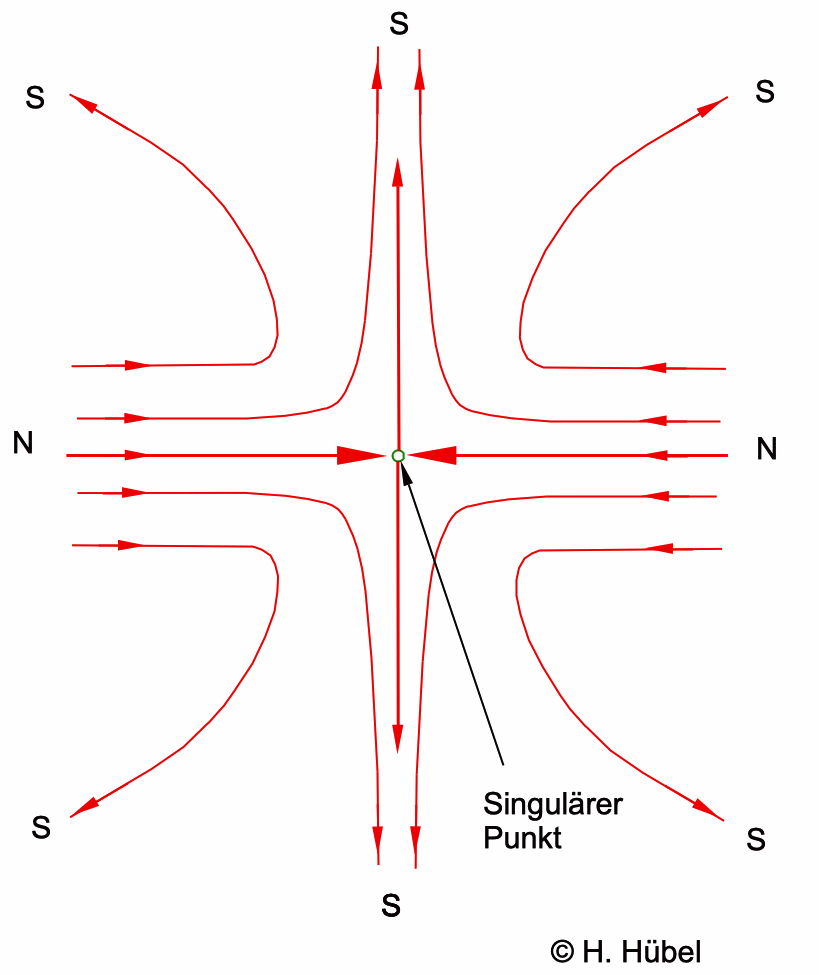
Abb. 2: Schematischer Verlauf der (gedachten) Feldlinien für zwei sich gegenüberstehende Stabmagneten oder entsprechend orientierte Helmholtz-Spulen im symmetrischen Fall. In diesem Fall gibt es eine Symmetrieebene senkrecht zur (horizontal gezeichneten) Symmetrieachse. In ihr gibt es ein ganzes Bündel von Feldlinien, die vom singulären Punkt wegstreben oder zu ihm hin. Zwei Feldlinien auf der Symmetrieachse nähern sich zwar dem singulären Punkt oder entfernen sich von ihm bei anderer Orientierung, aber sie erreichen ihn nie oder gehen nie von ihm aus. Das gleiche gilt für alle Paare entgegengesetzter singulärer Feldlinien in der Symmetrieebene. Am singulären Punkt selbst ist kein Magnetfeld, also auch keine Feldlinie. Deshalb haben auch solche Feldlinien weder Ende noch Anfang.

Es wird behauptet, dass dieser singuläre Punkt entweder der Endpunkt (!) zweier entgegengesetzter Feldlinien sei oder ihr Anfangspunkt (je nachdem, welche Pole sich annähern). Damit glaubt man die Behauptung widerlegen zu können, dass div B = 0 stets das Fehlen von Anfangs- und Endpunkt einer Feldlinie ausschließe.

Was bedeutet div B = 0 in einem Punkt? Um das zu erklären, wird üblicherweise der Punkt von einer geschlossenen Oberfläche umschlossen, z.B. einem Würfel, deren Dimensionen gegen 0 streben. Es wird der gesamte magnetischer Fluss durch die Oberfläche betrachtet, also der Überschuss zwischen eintretendem und der austretendem Fluss. Wenn dieser Gesamtfluss beim Grenzübergang gegen eine Konstante strebt, ist er ein Maß für div B. Wenn er verschwindet, erfüllbar z.B. durch das Gleichgewicht von eintretendem und austretendem Fluss, oder wenn kein Fluss ein- und austritt, ist div B = 0.

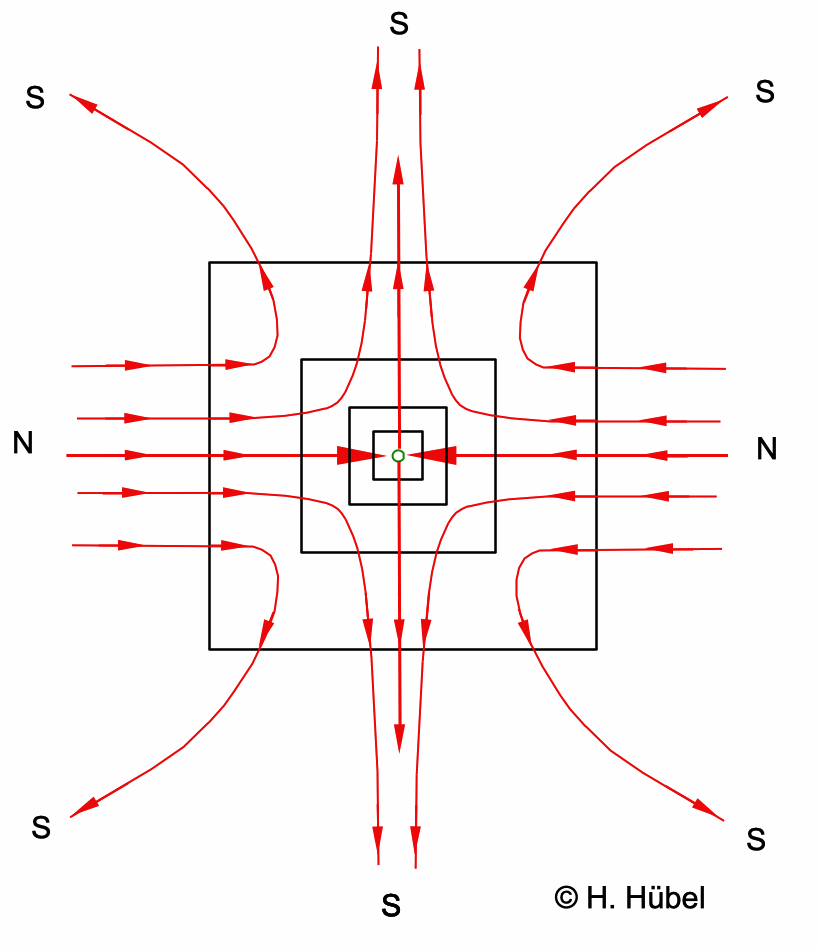
Abb. 3: Durch die Anzahl der Feldlinien wird symbolisiert, dass für jeden umschließenden Würfel (Quadrat) der eintretende magnetische Fluss genauso groß ist wie der austretende. Daran ändern die in Richtung singulärem Punkt oder in eine Richtung weg von ihm laufenden Feldlinien nichts. Das ist die eine Möglichkeit, wie sich div B = 0 für ein Magnetfeld B erfüllen lässt. Auf die Nichtexistenz von magnetischen Ladungen als Quellen oder Senken des magnetischen Felds lässt sich so nicht schließen. Das ist eine experimentelle Tatsache. Aber: Gäbe es Quellen oder Senken des magnetischen Felds, also magnetische Ladungen, könnte ein Überschuss des aus- bzw. eintretenden magnetischen Flusses existieren, also div B =/= 0.

In Abb. 3 tragen auch vom singulären Punkt ausgehende bzw. entsprechend zum singulären Punkt hin eintretende Feldlinien nie zum magnetischen Fluss durch die Oberfläche eines umschließenden Würfels (eines umgebenden Quadrats) bei. Die zugehörigen Feldlinien streben zwar zum singulären Punkt hin,  erreichen ihn aber nie bzw. streben von ihm weg, ohne von ihm auszugehen.

Diese Überlegungen wurden angestoßen durch einen Einwand eines aufmerksamen Lesers gegen meine falsche Behauptung, dass magnetische Feldlinien immer ringförmig geschlossen seien, eine Behauptung, die in den meisten Schul- und Hochschulbüchern zu finden ist. Der Leser schickte mir auch Kopien von wissenschaftlichen Veröffentlichungen dazu. Dafür und für die Diskussionen danke ich ihm sehr. Meine Überlegungen hier stützen sich überwiegend auf die Arbeit "L. Zilberti, The Misconception of Closed Magnetic Flux Lines, IEEE Mag. Lett. 8 (2017)". Ich habe meine Behauptung, auf einfache symmetrische Situationen einschränkend, wie sie in der Schule ausschließlich vorkommen, korrigiert. In diesem Text soll der Leser informiert werden, dass es auch andere Fälle gibt, die in modernen Anwendungen eine große Rolle spielen.

( November 2021 )