|
. . |
Physik für Schülerinnen und Schüler Wechselstrom durch Parallel-Schwingkreis © H. Hübel Würzburg 2021 |
Empfohlene Glossarthemen: |
Impres-sum |
|
|
I
Vorüberlegungen (zurück
zur Übersicht)
Wenn an eine Parallelschaltung von Spule und Kondensator eine Wechselspannung angelegt wird, muss man einige Besonderheiten erwarten. Die Wechselstrom-Widerstände beider Bauteile sind frequenzabhängig, aber in ganz unterschiedlicher Weise. Während der Wechselstrom-Widerstand der Spule mit zunehmender Frequenz wächst, nimmt er beim Kondensator mit zunehmender Frequenz ab. Dazwischen wird es eine Frequenz geben, bei der beide Wechselstrom-Widerstände gleich sind. Bei einem festen Maximalwert (einer festen Amplitude) der Spannung wird dementsprechend der Maximalwert der Stromstärke bei der Spule sinken und beim Kondensator wachsen. Dazwischen könnte es wieder eine Frequenz geben, bei der beide Stromstärken gleichen Maximalbetrag haben. Aber zu einem festen Zeitpunkt haben die beiden Ströme auch unterschiedliche Richtungen, ganz anders als bei einer entsprechenden Gleichstromschaltung. In Spule und Kondensator fließt dann z.B. ein Kreisstrom, der nicht von einer Stromquelle kommt!
(Die Maximalwerte heißen auch Scheitelwerte oder Amplitude.)
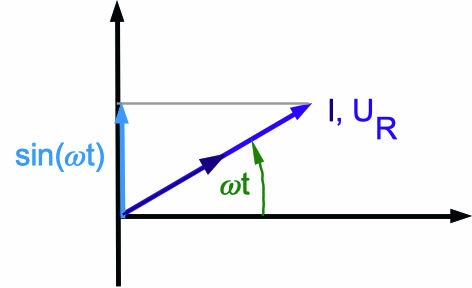
In einem Wechselstromkreis sind Stromstärke I(t) und Spannung U(t) zeitabhängig, z.B. sinusförmig. Man stellt sie als Zeiger dar, die in einem rechtwinkligen Koordinatensystem um den Koordinatenursprung mit der Kreisfrequenz ω = 2π ·f rotieren. f = 1/T ist dabei die Frequenz, T die Periodendauer. Wenn U(t) = U0·sin(ω·t) bei einer konstanten Amplitude U0, rotiert die Spitze des Zeigers auf einem Kreis mit dem Radius U0 um den Koordinatenursprung. Es wird vereinbart, dass der Drehwinkel/die Drehung mit ω·t = 0 an der horizontalen Achse beginnt. Die Projektion des Zeigers auf die vertikale Achse stellt dann den momentanen Wert der Spannung dar. Wenn nur ein Ohm'scher Widerstand im Kreis liegt, sind U(t) und I(t) "in Phase", d.h. beide sind proportional zu sin(ω·t). Ihre Zeiger sind stets parallel und rotieren gemeinsam um den Koordinatenursprung.
 |
Abb. 1: Am Zeigerdiagramm eines Ohm'schen Widerstands erkennt man anschaulich, wie sich die Stromstärke I(t) und die Spannung U(t) = UR gleichphasig verändern. UR ist hier der einzige Spannungsabfall im Wechselstromkreis. |
Wird der Ohm'sche Widerstand durch einen Kondensator mit der Kapazität C ersetzt, so sind U(t) und I(t) nicht mehr "in Phase". Aus Q = C·U ergibt sich nämlich durch Zeitableitung I = C·dU/dt = C·U· . I(t) = I0·sin(ω·t) erhalten wir nur dann, wenn U(t) = - U0·cos(ω·t) [mit I0 = U0·ω·C woraus sich der Wechselstrom-Widerstand ZC = U0/I0 = 1/(ω·C) ergibt]. I eilt dann der Spannung um 900 voraus, weil erst ein Strom fließen muss, bevor sich am Kondensator eine Spannung ausbilden kann.
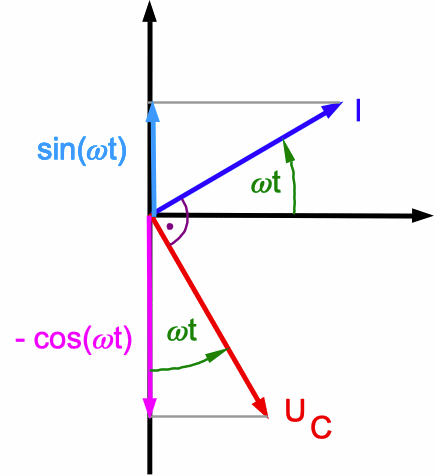 |
Abb. 2: Am Zeigerdiagramm des Kondensators
erkennt man anschaulich, dass I(t) der Spannung U(t) = UC
voraus eilt. Es muss erst ein Strom fließen, bevor sich eine
Spannung am Kondensator ausbilden kann. (UC ist hier der
einzige Spannungsabfall im Wechselstromkreis.) Der Wechselstrom-Widerstand des Kondensators ist ZC = 1/(ω·C). |
Für den Spannungsabfall an einer idealen Spule gilt dagegen UL = L · dI/dt. Bei sinusförmigem Strom folgt UL = L·ω·I0·cos(ω·t) und der Wechselstrom-Widerstand ZL = ω·L (entsprechend einer Selbstinduktionsspannung Uind = - UL ).
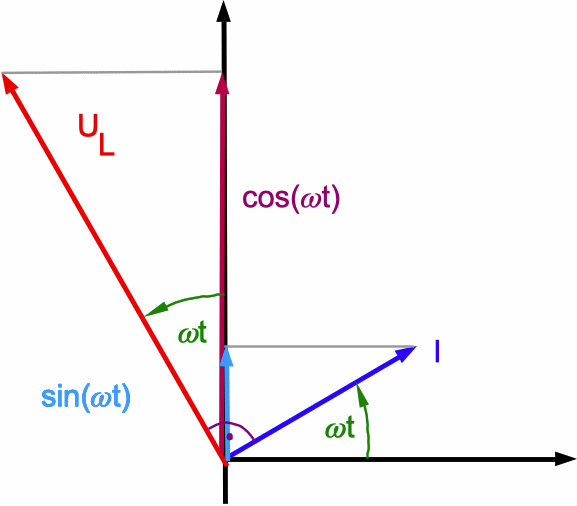 |
Abb. 3: Am Zeigerdiagramm der idealen Spule erkennt
man anschaulich, dass die Spannung U(t) = UL der
Stromstärke I(t) vorauseilt. (UL ist hier der einzige
Spannungsabfall im Wechselstromkreis.) Der Wechselstrom-Widerstand der idealen Spule ist ZL = ω·L. |
Durch eine Reihenschaltung (Serienschaltung) mehrerer Bauteile fließt immer der gleiche Strom. Deswegen kombiniert man dort mehrere Zeiger bezogen auf den gleichen Strom I.
III Parallelschaltung von idealer Spule und Kondensator: der ideale Parallelresonanzkreis (zurück zur Übersicht)
Was haben dagegen eine ideale Spule und ein parallel geschalteter Kondensator gemeinsam? An beiden liegt die gleiche Spannung, im einfachsten Fall die äußere Spannung U(t). Wir gehen also von ihr aus und kombinieren die unterschiedlichen Stromstärken IC(t) und IL(t) entsprechend der Regeln des Zeigerdiagramms. Die Resultierende beider Stromstärken ist dann der Gesamtstrom I(t), der durch die Parallelschaltung fließt.
Das Zeigerdiagramm des Kondensators muss dazu gegenüber dem Fall der Serienschaltung um 900 gedreht werden, das der idealen Spule um 2700 oder - 900. Wegen U(t) = UL(t) = UC(t) sind dann beide Spannungszeiger identisch.
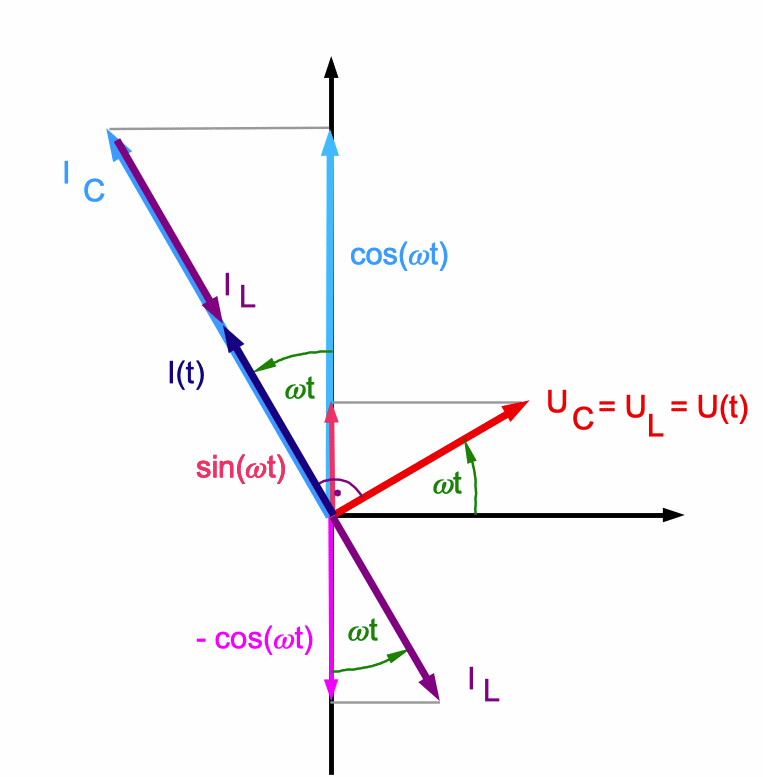 |
Abb. 4: Aus dem Zeigerdiagramm der idealen Spule
kombiniert mit dem Zeigerdiagramm des Kondensators ergibt
sich bei einer Parallelschaltung der resultierende Gesamtstrom I(t). Bei der Frequenz der Zeichnung eilt die Gesamtstromstärke I(t) der Spannung U(t) um 900 voraus. |
Folgerungen:
1. Bei gleicher Spannung an Kondensator und Spule sind die Ströme in beiden Zweigen "gegenphasig" (entgegengesetzt). Es ist möglich, dass aus der Stromquelle ein von 0 verschiedener Strom I(t) fließt (dunkelblau).
2. Wenn U(t) = U0·sin(ω·t), sind die Stromstärken in beiden Zweigen phasenverschoben gegenüber der Spannung, also prop. + cos(ω·t) [IC: blau] bzw. - cos(ω·t) [IL: violett] .
3. Wenn die Ströme in beiden Zweigen entgegengesetzt gleich sind, fließt aus der Stromquelle kein Strom [I(t) = 0]. Dann hat die Parallelschaltung beliebig hohen Wechselstrom-Widerstand. Sie wirkt als "Sperrkreis", weil sie keinen Strom durchlässt.
Wie ist das möglich, obwohl die Teilströme in beiden Zweigen von 0 verschieden sind? Das Schaltbild verrät es: Der Strom fließt ausschließlich zwischen Spule und Kondensator hin und her, also aus der Spule zum Kondensator und von diesem zurück zur Spule. Da Widerstände vernachlässigt werden, werden auch Energieverluste in ihnen vernachlässigt. Es ist kein weiterer Antrieb für diesen Vorgang nötig: Ein einmal angestoßener Stromfluss im Stromkreis Spule-Kondensator-Spule fließt ungeschwächt immer weiter. In einer realen Spule mit Widerstand muss das modifiziert werden.
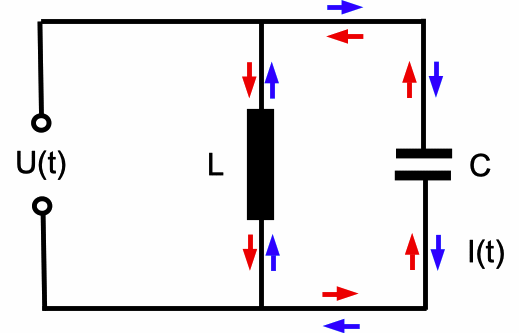 |
Abb. 5: Der Strom bleibt im Resonanzfall auf den Kreis Spule-Kondensator-Spule beschränkt. Ohne Widerstand fließt er verlustlos ohne weiteren Antrieb längs der roten Pfeile und zu anderen Zeiten längs der blauen Pfeile, natürlich nur, wenn Widerstände, vor allem in der Spule, vernachlässigbar sind. |
4. Resonanz tritt also ein, wenn | IL | = | IC |, also wenn UL(t)/ZL = UC(t)/ZC bzw. ZL = ZC, also wenn ω·L = 1/(ω·C) bzw. ω2 = 1/(L·C).
| ω0 = 1/√(L·C) |
ist die schon von der Serienresonanz bekannte Resonanzfrequenz.
Der Wechselstrom-Widerstand des LC-Gliedes ergibt sich aus den Stromstärken in der Parallelschaltung:
a) Für ω < ω0 überwiegt der Spulenstrom gegenüber dem Kondensatorstrom, also für den Betrag des Gesamtstroms:
I0 = IL0 - IC0 = U0/ZL - U0/ZC = U0/Z, und damit
1/Z = 1/ZL - 1/ZC = 1/ω·L - ω·C = (1 - ω2 L·C)/ω·L = (1 - ω2/ ω02)/ω·L, also
Z = ω·L / (1 - ω2/ ω02) = L/(1/ω - ω/ω02) = L/(1/ω - ω·L·C) = 1/[1/(L·ω) - ω·C] > 0.
b) Für ω > ω0 überwiegt der Kondensatorstrom gegenüber dem Spulenstrom, also für den Betrag des Gesamtstroms: Z = 1/ [ω·C - 1/(L·ω)] > 0.
c) Für ω = ω0 sind beide Ströme gleich, und es gilt: 1/Z = 0.
Für ω => ω0 strebt Z => ∞.
Für den Resonanzfall ω => ω0 wächst Z über alle Grenzen. Das bestätigt wieder die Funktion des LC-Gliedes als "Sperrkreis". Für ω => 0 (Fall a) strebt Z wie ZL gegen 0, für ω => ∞ (Fall b) strebt Z wie ZC gegen 0.
Jetzt schon lässt sich sagen: Ein endlicher Spulenwiderstand wird dafür sorgen, dass Z für ω => 0 endlich bleibt. Für die Ströme im Resonanzfall können wir erwarten, dass sie größere Amplitude haben können (von größerem Betrag sein können) als der von außen zufließende Strom, weil dieser nur benötigt wird, um die (kleinen) Energieverluste im Ohm'schen Widerstand auszugleichen.
IV Vergleich von Parallel- und Serienresonanz (zurück zur Übersicht)
| Serienresonanz | Parallelresonanz |
| gleiche Resonanzfrequenz ω0 = 1/√(L·C) | gleiche Resonanzfrequenz ω0 = 1/√(L·C) |
| Spannungen im Resonanzfall entgegengesetzt gleich: "heben sich gegenseitig auf": Resonanz in der Stromstärke | Ströme im Resonanzfall entgegengesetzt gleich bzw. sie bilden Kreisstrom durch L und C; Resonanz in der Spannung |
| Für ω => ω0 strebt Z => 0 (wenn kein Ohm'scher Widerstand) | Für ω => ω0 strebt Z => ∞ (wenn kein Ohm'scher Widerstand) |
| Gesamt-Spannung U(t) ≠ 0 im Resonanzfall nur, um Energieverluste auszugleichen. Die Schwingung findet (im Prinzip) ohne externen Antrieb statt. | Gesamt-Strom I(t) ≠ 0 im Resonanzfall nur, um Energieverluste auszugleichen. Die Schwingung findet (im Prinzip) ohne externen Antrieb statt. |
| saugt bei der Resonanzfrequenz einen (großen) Strom durch den Wechselstromkreis ("Saugkreis") | sperrt bei der Resonanzfrequenz den Strom ("Sperrkreis") |
Beide LC-Kreise lassen sich auch auffassen als Schwingkreise, die von
außen zu erzwungenen Schwingungen angeregt werden.
Die Gesetzmäßigkeit für eine Parallelschaltung im Gleichstromfall ist hier nicht anwendbar, weil dort in beiden Zweigen gleichgerichtete Ströme vorausgesetzt werden.
( Januar 2021 )