.

Zu einer Kraft F sollen zwei Teilkräfte mit gleichem Angriffspunkt gefunden werden, die  zusammen die gleiche Wirkung haben wie die Kraft F.

.

1. Schritt	Hier lernst du, wie man eine solche Kräftezerlegung zeichnerisch durchführt, vor allem aber, welche Richtungen man für die Teilkräfte wählt.
2. Schritt	Hier lernst du, wie man mit einer solchen Kräftezerlegung physikalische und technische Fragen klären kann. Du lernst auch, wie man die Verhältnisse (Quotienten) aus den Beträgen der Kraft und von Teilkräften durch Streckenverhältnisse ausdrücken und so sogar ohne Zeichnung rechnerisch bestimmen kann.
3. Schritt	Hier lernst du, wie man bei verschiedenen Fragestellungen in Physik und Technik die Teilkräfte aus der zerlegten Kraft und den gewählten Winkeln einfach ohne Zeichnung ausrechnen kann.
4. Schritt	Hier solltest du mit Kräftezerlegungen wie im Schlaf umgehen können. Du brauchst sie, weil verschiedene Fragestellungen der Mechanik nur mit Kräftezerlegungen gelöst werden können. Du wirst von einer Skizze ausgehen, aus der die gewählten Richtungen hervorgehen. Bestimmen wirst du die Teilkräfte aber immer mit rechnerischen Methoden.

1. Schritt:

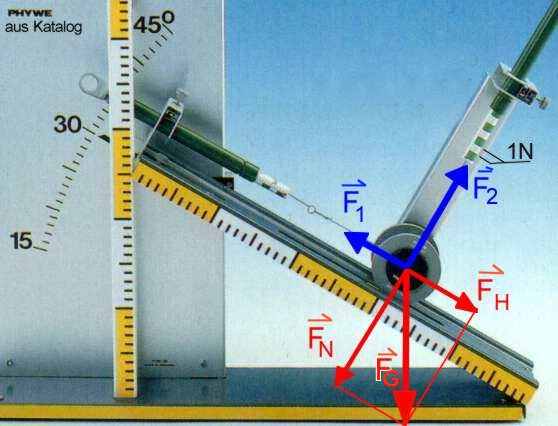Grundexperiment zur Kräftezerlegung an der Schiefen Ebene (rot) Die Gewichtskraft FG spielt hier die wichtigste Rolle. Ohne Gegenkräfte (blau) bewirkt sie, dass die Rolle hangabwärts gezogen wird, und dass diese senkrecht auf die Unterlage gedrückt wird. Sie wird deshalb zerlegt in die Hangabtriebskraft FH und die Normalkraft FN Die Federkräfte F1 und F2 halten das Gleichgewicht zu FH bzw. FN, wenn sich der Gleichgewichtszustand eingestellt hat

Das folgende Video zeigt, wie die Kräftezerlegung durchgeführt wird:  (Evtl. musst Du mit der Maus das Bild anklicken!)

a) nach der Methode des Kräfteparallelogramms (oder in GIF-Format: Kräfteparallelogramm)

b) nach der Methode des Kräftedreiecks (oder in GIF-Format: Kräftedreieck)

Du kannst aber keine Kräftezerlegung sinnvoll durchführen, bevor Du Dich nicht für die richtige Wahl der Teilkräfte (Kraftkomponenten) entschieden hast. Im Prinzip könnten für die Teilkräfte fast jede beliebige Richtung gewählt werden. Aber nur bei einer bestimmten Wahl kann man mit der Zerlegung ein physikalisches Problem lösen. Und darauf kommt es uns ja an!

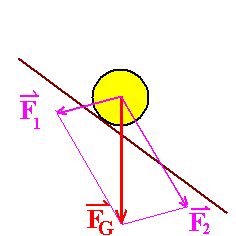Auch das wäre eine richtige Zerlegung der Gewichtskraft FG in die zwei Teilkräfte F1 und F2 Man kann mit ihr aber überhaupt nichts anfangen! F1 enthält noch einen Anteil, der längs der schiefen Ebene nach oben zieht, F2 einen Anteil, der längs der schiefen Ebene nach unten zieht. Schade um die Mühe!

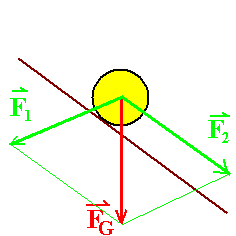Noch eine richtige Kräftezerlegung, mit der man nichts anfangen kann! F2 enthält jetzt nur einen Anteil parallel zur schiefen Ebene. Der eine Fehler vom letzten Diagramm ist jetzt behoben. Aber F1  enthält immer noch einen Anteil längs der schiefen Ebene, und zwar nach oben. F2 kann also trotz der korrekten Richtung nicht die Hangabtriebskraft sein! Schade um die Mühe! Erst, wenn man die Richtungen so wählt wie in der obersten Zeichnung, enthält FH ausschließlich die Anteile parallel zur Schiefen Ebene und FN keine. FN ist dann genau senkrecht zur Fahrbahn gerichtet.

Im Beispiel zu Regel 1 ist die untersuchte Wirkung die Beschleunigung der Kugel längs der schiefen Ebene den Hang hinab.

Zu Regel 2 ist ein Beispiel der Keil, mit dem man z.B. ein Stück Holz spaltet.

	Olivfarben ist das Holz dargestellt, türkis der Keil. Schlägt man auf die Breitseite des Keils, dringt der Keil in das Holz ein und drückt das Holz seitlich weg.
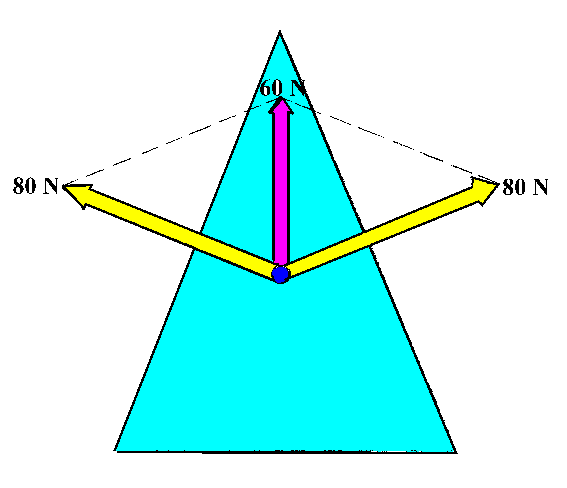	Damit ist klar, was eine gewünschte Wirkung sein wird, nämlich Kräfte senkrecht zu den Seitenflächen des Keils; denn durch sie wird das Holz gesprengt. Man wählt also zwei Komponenten senkrecht zu den Seitenflächen des Keils. Die nebenstehende Figur zeigt die Kräftezerlegung.
Schmaler Keil	Was soll man aber mit einer solchen Konstruktion anfangen? Nur, wenn man ein physikalisches Problem lösen kann, lohnt sich die Mühe. Eine Fragestellung wäre z.B., wie man das Holz mit der gleichen Kraft auf den Keil (violett) wirksamer spalten könnte, oder wie man mit einer kleineren violetten Kraft die gleiche Wirkung hervorrufen könnte. Wenn du den Link links anklickst, wirst du eine Graphik sehen, die dir weiterhilft. Was schließt du aus der Graphik ?

Hier kannst du die Wahl der Richtungen  - je nach der physikalischen Fragestellung - in weiteren Situationen trainieren.

2. Schritt

Hier erfährst du,

• wie man rechnerisch das Verhältnis F_N/F_G aus den Abmessungen der schiefen Ebene, und
• wie man rechnerisch das Verhältnis F_H/F_G aus den Abmessungen der schiefen Ebene ermitteln kann,
• wie man die Reibungskraft F_R bzw. die Haftkraft F_Haft  aus den Abmessungen der schiefen Ebene ermitteln kann, oder
• wie man die Haftzahl f_H oder µ_H mit Hilfe einer schiefen Ebene bestimmen kann.

Immer ist es nötig, sich in einer Skizze über die zu wählenden Komponenten der Gewichtskraft klar zu werden. Dann aber kann man sehr einfach das gewünschte Ergebnis errechnen.

Um die Verhältnisse F_N/F_G  und F_H/F_G zu ermitteln, könnte man Versuche machen. Vielleicht hast du das in den Physik-Übungen gemacht oder wirst es noch machen. Man kann sie aber auch mathematisch herleiten.

Schlüssel dazu ist die Ähnlichkeit der Dreiecke ΔABC und ΔA'B'C'. Die Dreiecke sind ähnlich, weil sie in 2 Winkeln übereinstimmen, dem rechten Winkel und dem Winkel α. Dieser tritt in beiden Dreiecken auf, weil Winkel, deren Schenkel paarweise aufeinander senkrecht stehen, gleich sind, oder sich zu 180º ergänzen.

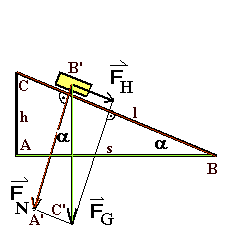Begründung, dass der Winkel α in beiden Dreiecken ΔABC und ΔA'B'C' auftritt, und dass deshalb die beiden Dreiecke ähnlich sind.

In ähnlichen Dreiecken sind die Verhältnisse einander entsprechender Strecken gleich, also gilt:

(1)     F_N/F_G = s/ℓ

(2)     F_H/F_G = h/ℓ

aus beiden zusammen folgerst du, wenn du (1) durch (2) dividierst:

F_N/F_H = s/h

Ist ja schön, dass man solche Verhältnisse aufstellen kann; aber kann man damit physikalische Probleme lösen?

Klar, sonst würde man ja nicht so viel Aufwand treiben!

• Aus (1) folgt z.B., dass bei fester Gewichtskraft F_G die Normalkraft F_N umso größer ist, je größer die Strecke s, also je flacher die schiefe Ebene ist.

• Aus (2) folgt z.B., dass bei fester Gewichtskraft F_G die Hangabtriebskraft F_H umso größer ist, je größer die Strecke h, also je steiler also die schiefe Ebene ist.

  Das hättest du ohnehin gewusst; es entspricht ja schließlich deiner Erfahrung!

• Du kannst auch wieder einmal bestätigen, dass man mit der schiefen Ebene keine Arbeit sparen kann, dass die Goldene Regel also auch hier gilt:

  (3) Beim direkten Heben um die Höhe h muss gegen die Gewichtskraft F_G die Arbeit F_G· h = m·g·h verrichtet werden.

  (4) Beim Hochschieben längs der schiefen Ebene um die Strecke ℓ muss die Arbeit F_H· ℓ verrichtet werden. Wegen (1) gilt für sie: F_H· ℓ = F_G·h/ℓ · ℓ = F_G·h . Also ist die Verschiebungsarbeit in beiden Fällen gleich.

• Es ergibt sich auch eine sehr elegante Möglichkeit, die Haftzahl zu bestimmen. Lege dazu den Körper auf die schiefe Ebene und mache sie vorsichtig immer steiler, bis der Körper gerade zu rutschen beginnt. Zuvor ist die Haftkraft immer größer als die Hangabtriebskraft: der Körper wird festgehalten. Die Grenze zwischen "gerade noch festgehalten" und "sich gerade in Bewegung setzend" ist durch das Kräftegleichgewicht bestimmt:    F_Haft = F_H .

  Wegen  F_Haft = f_H · F_N  und    F_Haft = F_H  gilt also:

                                f_H =  F_H / F_N = h/s

  Du brauchst also nur noch h und s zu messen, wenn sich der Körper gerade in Bewegung setzt, und erhältst daraus die Haftzahl f_H.

3. Schritt

Grundbeispiel ist wieder die Kräftezerlegung an der schiefen Ebene. Wie das zeichnerisch zu machen ist, sollte dir klar sein. Mit Hilfe der trigonometrischen Funktionen lassen sich aber ohne Zeichnung, nur mit Hilfe einer Skizze, rechnerisch zuverlässige Aussagen machen.

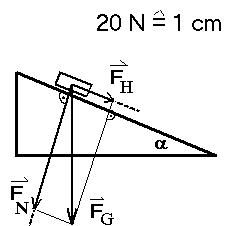Fragestellungen: Wie groß ist bei vorgegebener Gewichtskraft und Bahnneigung α die Hangabtriebskraft FH oder die Normalkraft FN (die die Reibungskraft bestimmt)? Wie kann man es einrichten, dass der Körper auf der schiefen Ebene durch eine größere Kraft hangabwärts beschleunigt wird?

Rechnerische Lösung: Im rechtwinkligen Dreieck ergibt sich: FH = FG · sin(α) = m·g · sin(α) FN = FG · cos(α) = m·g · cos(α) . Hier müssen noch die jeweiligen Zahlenwerte eingesetzt werden. Man kann aber schon ohne jede Rechnung sehen: Weil sin(α) mit zunehmender Bahnneigung α wächst, wächst auch die Hangabtriebskraft dabei. Weil cos(α) mit zunehmender Bahnneigung α fällt, wird auch die Normalkraft und damit die Reibungskraft mit zunehmendem Winkel α immer kleiner.

Ähnliche trigonometrische Rechnungen lassen sich auch bei allen anderen Beispielen zur Kräftezerlegung durchführen.

4. Schritt

Grundbeispiel soll wieder die Kräftezerlegung an der schiefen Ebene sein. Du weißt, wie man die Richtungen der Kraftkomponenten - passend zur Fragestellung - wählt, du kannst eine Skizze zur Kräftezerlegung anfertigen, und du weißt, wie man die Kraftkomponenten mit Hilfe von trigonometrischen Funktionen berechnet. Andernfalls müsstest du oben noch einmal nachlesen.

Wende deine Kenntnisse nun zur Lösung von physikalischen Problemen an:

Fragestellung: Auf einer schiefen Ebene kann ein Körper der Masse m bei genügender Hangabtriebskraft gleiten. Gegeben sind Reibungszahl fR = 0,05 und Haftzahl fH = 0,15 (vielleicht kennst du beide unter den Abkürzungen µR und µH ). Die Masse soll m = 0,10 kg sein, aber sie hat keinen Einfluss. a) Bei welcher Bahnneigung setzt sich der zunächst ruhende Körper hangabwärts in Bewegung? b) Welche Beschleunigung erfährt er nach dem er sich in Bewegung gesetzt hat, bei α = 30º? c) Nach welcher Zeit t nach dem Start erreicht er das Ende der schiefen Ebene bei d = 1,0 m ?

Überlegungen zur Lösung: a) Solange der Körper noch ruht, wird er durch die Haftkraft festgehalten. Diese kann bis auf einen maximalen Wert ansteigen, wenn die Hangabtriebskraft immer mehr erhöht wird. Die Größe der Haftkraft ist durch die Normalkraft bestimmt, mit der der Körper senkrecht auf seine Unterlage, also auf die schiefe Ebene,  gedrückt wird. Der Körper beginnt, sich in Bewegung zu setzen, wenn beide Kräfte gleich groß sind. (Wir könnten auch sagen, dass er in diesem Fall gerade noch durch die Hangabtriebskraft festgehalten wird). Es ist also der Winkel zu berechnen, bei dem Kräftegleichgewicht zwischen Haftkraft und Hangabtriebskraft eintritt. b) Sobald der Körper in Bewegung geraten ist, wirkt nur mehr die kleinere Gleitreibungskraft. Die Hangabtriebskraft wird überwiegen. Beschleunigt wird der Körper durch die Gesamtkraft längs der schiefen Ebene. Die Reibungskraft ergibt sich wieder aus der Normalkraft, mit der der Körper auf die Unterlage gedrückt wird.

Lösung: Für Hangabtriebskraft und Normalkraft gilt: FH = FG · sin(α) = m·g · sin(α) FN = FG · cos(α) = m·g · cos(α) . Die maximale Haftkraft ergibt sich dagegen aus FN mittels:   FHaft = fH · FN = fH · m·g · cos(α) . Beim Gleiten gilt ganz entsprechend für die (Gleit-)Reibungskraft FR:   FR = fR · FN = fR · m·g · cos(α) . Zu a) Die Grenze zwischen "gerade noch festgehalten" und "sich gerade in Bewegung setzend" ist durch das Kräftegleichgewicht bestimmt:    FHaft = FH , also fH · m·g · cos(α) =  m·g · sin(α) .  m·g kürzt sich heraus, und du erhältst:   fH · cos(α) =  sin(α) . Das ist eine goniometrische Gleichung für α. Dummerweise kommt α auf beiden Seiten vor. Zum Glück kennst du aber die Definitionsgleichung des Tangens:   tan(α) = sin(α) / cos (α) . Du kannst sie ins Spiel bringen, wenn du beide Seiten durch cos(α) dividierst ( solange cos(α) ¹ 0 ). Es ergibt sich also:                           fH  =  tan(α) Die Masse ist ganz heraus gefallen! Für fH = 0,15  ergibt sich mit dem Taschenrechner (tan-1) :          α  = 8,5º Zu b): Als Gesamtkraft hangabwärts ergibt sich, wenn der Körper bereits gleitet,  FH - FR = m·g · sin(α) - fR · m·g · cos(α) = m·g·[ sin(α) - fR · cos(α) ]. Du siehst wieder: Diese Kraft ist größer als 0, bewirkt also eine positive Beschleunigung hangabwärts, wenn sin(α) - fR · cos(α) > 0 . Das ist dann der Fall, wenn tan(α) > fR . Da fR < fH  kann das bei einem Neigungswinkel geschehen, bei dem der ruhende Körper noch auf der Unterlage haften würde.

Zur Wahl der Richtungen je nach der physikalischen Fragestellung:

Wie bereits gesagt: Zu einer bestimmten Kraft gibt es beliebig viele richtige Kräftezerlegungen, je nach der Wahl der Richtungen der Komponenten.

Physikalisch sinnvoll ist eine solche Kräftezerlegung aber nur, wenn man damit ein physikalisches Problem lösen kann. Im Folgenden lernst du also einige Argumente für die Wahl sinnvoller Richtungen kennen.

1. Kräftezerlegung an einer schiefen Ebene: Eine sinnvolle physikalische Fragestellung könnte sein: Mit welcher Kraft wird ein Körper auf der schiefen Ebene abwärts beschleunigt. Die zweite Kraftkomponente darf dann keinen Anteil in Richtung der Beschleunigung oder entgegengesetzt dazu enthalten, d.h. sie muss senkrecht zur Bahn stehen. Deshalb wird die eine Komponente gemäß der Regel 1 parallel zur schiefen Ebene, die zweite senkrecht dazu gewählt.

.

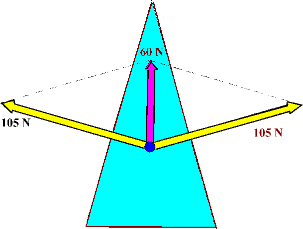
2. Kräftezerlegung am Keil: Eine sinnvolle physikalische Fragestellung könnte sein: Mit welcher Kraft presst der Keil das Holz auseinander, wenn auf ihn eine Kraft F (längs seiner Symmetrierichtung) wirkt? Die gewählten Kraftkomponenten sollen nur für das seitliche Pressen verantwortlich sein, nicht etwa auch dafür, dass der Keil in das Holz hinein getrieben wird. Deshalb wirken sie senkrecht zur Flanke des Keils. (Regel 2)

.

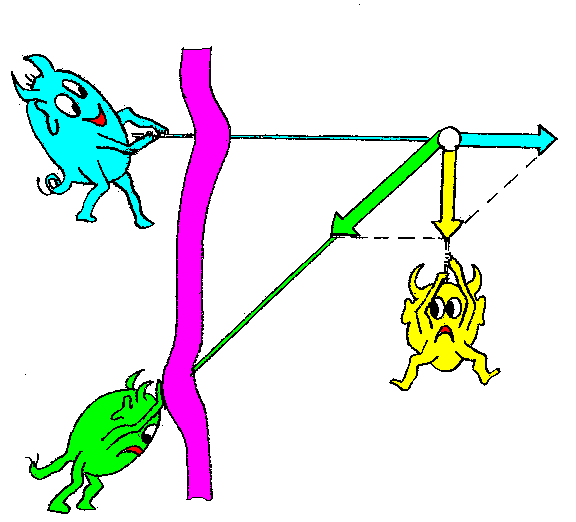3. Wirtshausschild: Es ist anschaulich klar, dass der horizontale Träger nach außen gezogen wird, und dass die schräge Strebe in die Wand hinein gedrückt wird. Eine sinnvolle physikalische Fragestellung könnte deshalb sein: Wird der horizontale Träger aus der Wand gezogen, wenn er maximal mit einer Kraft von 200 N in der Wand gehalten werden kann? Wird die schräge Strebe in die Wand gedrückt, wenn der Gips dort maximal 100 N aushält? Also: Mit welcher Kraft wird der horizontale Träger aus der Wand herausgezogen? Mit welcher Kraft wird die schräge Strebe in die Wand hinein gedrückt? Bei dieser Fragestellung ist es klar, dass eine Komponente längs des horizontalen Trägers nach außen gewählt werden muss, und die zweite Komponente längs der schrägen Strebe in die Wand hinein. (Regel 2)

.

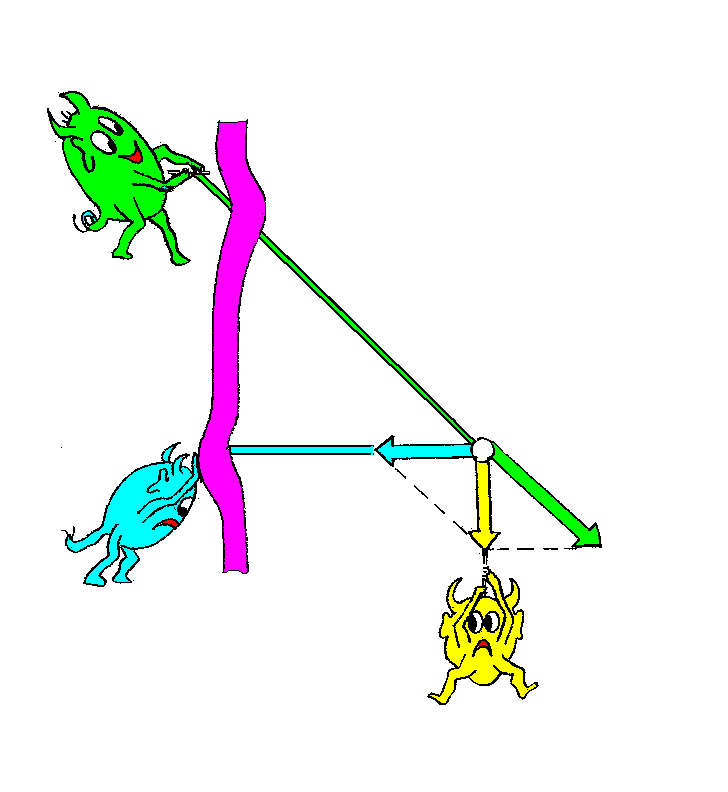
4. Regalbrett: Es ist anschaulich klar, dass das horizontale Brett in die Wand hinein gedrückt wird und dass am schrägen Träger von der Wand weg gezogen wird. Eine sinnvolle physikalische Fragestellung könnte deshalb sein: Mit welcher Kraft wird am schrägen Träger gezogen? Hält der Dübel bei einer maximalen Belastung von 200 N? Weniger spannend ist, mit welcher Kraft das Regalbrett in die Wand hinein gedrückt wird. Dennoch liegen dadurch die zu wählenden Richtungen fest. (Regel 2)

.

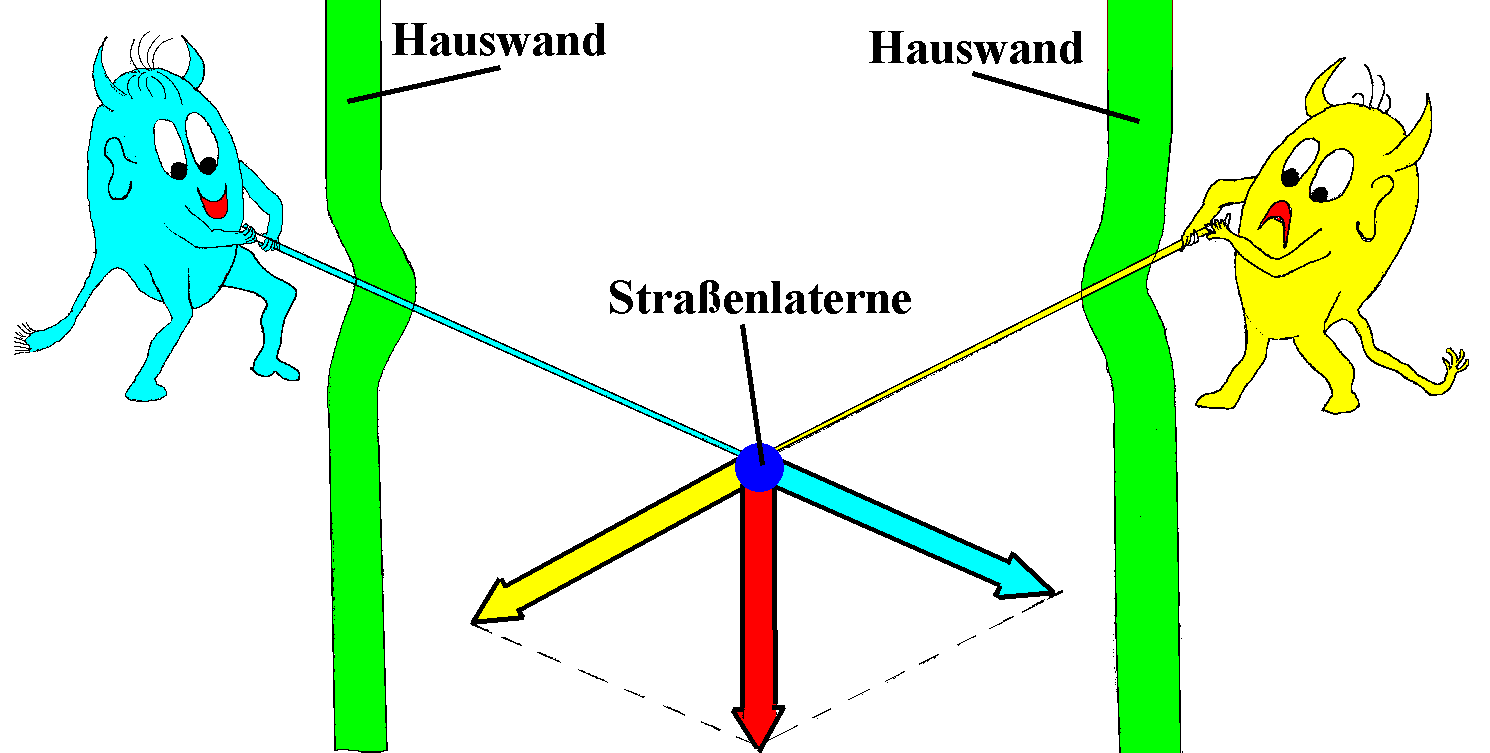5. Straßenlaterne: Physikalisch klar ist, dass längs der beiden Seile ein Zug entsteht, durch den vielleicht das Seil mit dem Dübel aus der Wand gerissen wird. Deshalb könnte eine sinnvolle physikalische Fragestellung sein: Mit welcher Kraft wird bei einem bestimmten Gewicht der Lampe längs der beiden Seilstücke an den Dübeln gezogen? Die Wahl der Kraftrichtungen längs der beiden Seile liegt damit fest. (Regel 2)

.

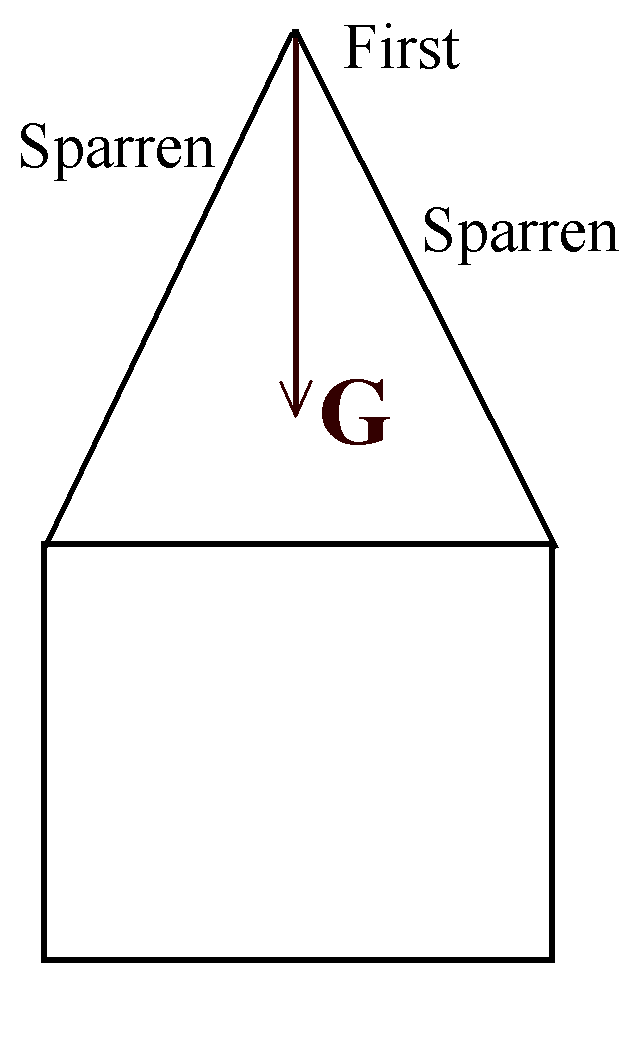
6. Kraft längs der Sparren eines Daches (vereinfacht): Auf einem Paar von Sparren lastet das Gewicht der Sparren selbst, das anteilige Gewicht des Dachfirstes und der Ziegeln etc. Ein Durchbiegen der Sparren soll vernachlässigt werden. Wir können näherungsweise alle diese Kräfte zu einer Gewichtskraft G zusammenfassen, die senkrecht nach unten wirkt und am Kreuzungspunkt der Sparren (First) angreift. Sie wird über die beiden Sparren "nach unten gelenkt". Damit liegen wieder zwei Richtungen fest. (Regel 2)

.

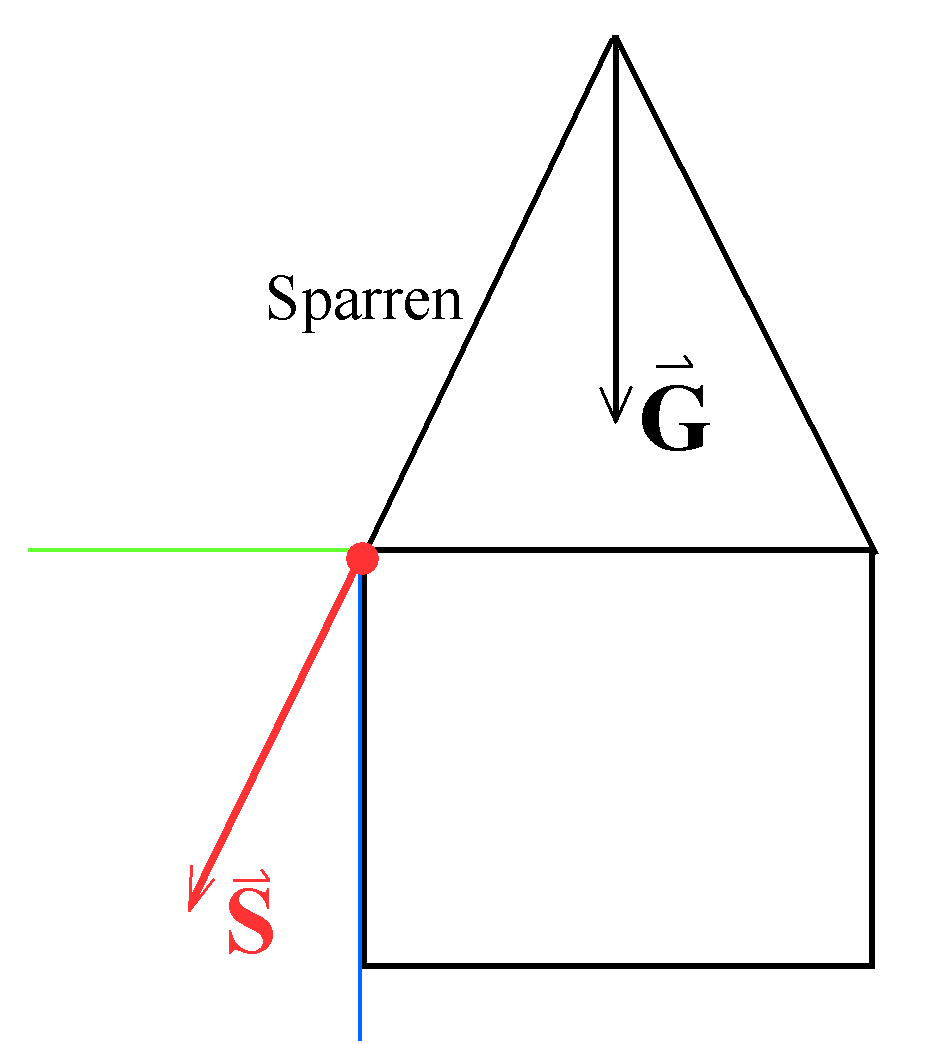
7. Auflagekraft der Sparren eines Daches (vereinfacht): Der schräge Sparren sitzt auf einer Mauer (oder einem horizontalen Balken). Eine sinnvolle physikalische Fragestellung könnte sein: Mit welcher Kraft FH wird die Mauer (der Balken) vom Sparren nach außen gedrückt? Wird eine maximale Kraft nicht überschritten? Welche Kraft FV drückt vertikal auf die Außenmauer? Die grüne und die blaue Kraftrichtung sind naheliegend für die Horizontalkraft FH und die Vertikalkraft FV. (Für die vertikale Kraft müsste bei einem symmetrischen Dachstuhl die Hälfte der Gewichtskraft G herauskommen.) (Regel 1)

.

8. Bohnerbesen Der Bohnerbesen wird längs des blauen Besenstiels gedrückt. Wozu macht man das? Natürlich um eine Kraft auf den Boden auszuüben (rot) und den Bohnerbesen (gelb) vorwärts zu treiben (grün). Damit liegen die beiden Kraftrichtungen fest (rot und grün). Eine nicht gerade umwerfende Fragestellung könnte sein: Wie muss man die Neigung des Besenstiels wählen, damit eine möglichst große Kraft auf den Boden ausgeübt wird? (Regel 1)

(2004 und 2013)