Korrekte Darstellung mathematischer Symbole unter Netscape ab Version 6

Was Sie erwartet:

• 1. Sprachregelungen über Wellen und Teilchen in der Quantenphysik
• 2. Was meine ich mit heuristischen Methoden?
• 3. Grundfakten der Quantenphysik und heuristische Methoden
• 4. Anwendungen der heuristischen Methoden in der Schule
• 5. Resümee
• 6. Eine Auswahl von Literatur und Links

Download der Präsentation als PDF-File (ca. 700 kB)

In den letzten Jahren wurden vereinfachte Rechen-Methoden für die Quantenphysik in der Schule diskutiert, die beeindruckende Ergebnisse liefern. Dazu gehört die Zeiger-Methode, die einerseits als eine vereinfachte Variante von Feynmans Pfadintegral-Methode gesehen werden kann, andererseits als elementarisierte Form der "Ausbreitung" Schrödingerscher Wellen(funktionen) - was auch immer das bedeuten sollte. Dazu gehören auch Verfahren, bei denen Simulationsprogramme die Schüler von Lösungsmethoden der Schrödinger-Gleichung entlasten, ihnen aber Kernpunkte der Schrödinger-Theorie eindringlich vor Augen stellen, insbesondere den Zusammenhang zwischen "Quadratintegrabilität" (vereinfacht zu Endlichkeit der Wellenfunktion) und der Existenz diskreter (Energie-)Eigenwerte. Zu letzterem Punkt seien die Programme Schrödingers Schlange von Küblbeck und ein ähnliches Programm von Bader erwähnt, zur Zeigermethode wird auf die vielen Programme Baders hingewiesen. So relativ einfach die erwähnten numerischen oder mathematischen Verfahren in den vorgeschlagenen Näherungen und Spezialfällen für Schüler sein dürften, so schwierig dürfte es für sie und die unterrichtenden Lehrer sein, die zugrunde liegende Physik zu verstehen. Ich fürchte, hier gerät der Lehrer in die Gefahr, den Rahmen der Schulphysik zu überschreiten. Weil die Programme so einfach zu benutzen sind, können m.E. ihre Ergebnisse dennoch eine wichtige Funktion im Unterricht haben.

Hier soll ein Konzept vorgestellt werden, wo mehr Wert auf ein Verständnis der Grundlagen gelegt wird. Das haben sich auch Wiesner, Müller und Küblbeck und andere zum Ziel gesetzt. Insbesondere von Küblbeck und Müller wurde zusätzlich zu bekannten heuristischen Verfahren eine Variante der Komplementarität als heuristisches Prinzip hervorgehoben und an vielen modernen experimentellen Beispielen erläutert. Es erscheint deshalb an der Zeit, zur Didaktik der Quantenphysik eine Rückbesinnung einzulegen, um sich zu vergewissern, wie eine Sicherheit in den Grundlagen des Gebiets gepaart mit einigen dieser heuristischen Methoden wesentliche experimentelle Situationen verständlich machen kann, ohne in die Gefahr zu geraten mit den diskutierten - zugegebenermaßen  vereinfachten - mathematischen Methoden den Blick auf das Wesentliche für die Schulphysik zu verstellen und offene physikalische Probleme zuzudecken.

Zur Begründung werde ich manchmal Beispiele vorführen, die über die Schulphysik hinausgehen. In der Regel möchte ich nicht, dass sie in die Schulphysik eingeführt werden.

1. Sprachregelungen über Wellen und Teilchen in der Quantenphysik

Dabei soll versucht werden, möglichst eindeutige Sprechweisen zu verwenden. So wird, wie das auch schon von Küblbeck und Müller praktiziert worden ist, kaum von Wellen gesprochen werden, die ja im Rahmen von Schrödingers Theorie in der Regel abstrakte Wellen in hochdimensionalen Konfigurationsräumen sind und eben nicht im Anschauungsraum, wie Schülern kaum auszureden sein wird, wenn man in diesem Zusammenhang von Wellen spricht. Die Bornsche Wahrscheinlichkeitsdeutung sollte aber behandelt werden.

Nehmen Sie ein Elektron. Wenn Sie Schrödinger-Theorie betreiben wollen, ist die zugehörige Wellenfunktion (ohne Berücksichtigung des Spins) eine Wellenfunktion in einem Raum, der wie der Anschauungsraum dreidimensional ist. Aber dieser Raum könnte der dreidimensionale Impulsraum sein, oder auch ein dreidimensionaler Ortsraum. In letzterem Fall sind die drei Koordinaten x,y,z nicht die Koordinaten eines Teilchens, sondern die Koordinaten des Punktes, an dem eine Messung  vorgenommen werden wird, deren wahrscheinlicher Ausgang durch die Wellenfunktion vorhergesagt werden soll. Nehmen Sie aber einen Zweiteilchen-Zustand, z.B. aus zwei Elektronen, dann ist der zugehörige Raum (ohne Spin) 6-dimensional, also ganz klar nicht der Anschauungsraum, sondern der 6-dimensionale Konfigurationsraum, zuständig ausschließlich für Wahrscheinlichkeitsvorhersagen. Nach Zeilinger existieren Wellenfunktion "nur im Kopf der Physiker".

Damit wir uns einig sind: Natürlich ist die Schrödinger-Gleichung eine Art Wellengleichung in Konfigurationsräumen für Teilchen-Zustände. Andererseits werden die Feldgleichungen  meistens sogar als Wellengleichungen im dreidimensionalen Ortsraum formuliert, aber für Operatoren! Aus ihnen lassen sich Informationen für Teilchen-Zustände und Nicht-Teilchen-Zustände entwickeln. Das geht m.E. über die Schulphysik weit hinaus und soll hier nicht besprochen werden. Die klassische Schrödinger-Theorie, nach der "Teilchen eigentlich Wellenpakete seien", in der Wellenfunktionen irgendwie als "reale" Wellen im Anschauungsraum angesehen wurden, ist seit Etablierung der Quantentheorie Ende der 20-er / Anfang der 30-er Jahre tot. Aber aus dieser Zeit haben sich leider noch viele irreführenden Sprechweisen erhalten: Elektronenbeugung, Materiewelle, Ladungswolke, "verschmierte Elektronen", das "Elektron im Atom als stehende Welle", aus der Übergangsphase auch "Aufenthaltswahrscheinlichkeit" statt "Nachweiswahrscheinlichkeit".

2. Was meine ich mit heuristischen Verfahren?

Das "heuristische Verfahren" steht ja in der Didaktik in hohem Kurs. Physiker benutzen das Wort "heuristisch" aber anders und meinen damit etwas anrüchig eher "hingebastelt" oder "unbegründet, aber wohl richtig" oder "aus der Luft gegriffen, aber passend". Sie bezeichnen damit Methoden, die sich nicht aus irgendeiner Theorie ergeben, aber doch in der Lage sind, Sachverhalte richtig in einer Theorie, in Rechnungen oder Simulationen abzubilden. Das Verfahren hat generell eine wichtige Funktion, wenn die ersten Schritte in einem neuen Forschungsgebiet gemacht werden, oder wenn, z.B. für die Anwendung in der Technik, eine empirische Regel aufgestellt werden soll, deren theoretische Begründung zu komplex ist oder nicht interessiert. So wird es auch hier der Begriff eher verwendet, aber in durchaus positivem Sinn:

Da sich die vorgeschlagenen heuristischen Verfahren aus der kompletten Quantentheorie ergeben sollen, sollen sie - so weit wie möglich - mit ihr in Einklang sein. Sie sollen dem Schüler aber aufwändige Rechnungen ersparen, sollen schneller, sozusagen auf einer Abkürzung richtige Ergebnisse liefern, häufig eher qualitative, die aber für die Schule durchaus ausreichen. Aber sie sollen mit der richtigen Quantentheorie so weit wie möglich verträglich sein.

Ich habe mir also folgende Forderungen an "vernünftige" heuristische Verfahren für die Schule gestellt:

• Sie sollen physikalische Sachverhalte treffend vor Augen stellen.
• Sie  und die erläuterten Sachverhalte sollen einfach sein.
• Sie sollen möglichst wenig im Widerspruch stehen zu anderen wichtigen Aussagen der Physik, insbesondere der Quantenphysik.

Heuristische Verfahren in der Quantenphysik sind für die Schule natürlich schon lange vorgeschlagen worden.

Beispiel 1:

Z.B. wird zu einer Behandlung des H-Atoms, die über das Bohrsche Modell hinausgehen soll, vorgeschlagen, die Grundzustandsenergie E aus einem Minimalprinzip zu bestimmen. E soll aus kinetischer und potenzieller Energie zusammengesetzt werden ( - obwohl wir wissen, dass das Elektron nicht gleichzeitig kinetische und potenzielle Energie haben kann). Die potenzielle Energie habe dabei die übliche -1/r-Abhängigkeit, die kinetische Energie wird abgeschätzt durch eine Un-be-stimmtheitsrelation Dp.Dr = h/2p, wobei dann die Ortsun-be-stimmtheit Dr durch den Atomradius r und die Impulsun-be-stimmtheit Dp durch den "Minimalimpulsbetrag" p ersetzt wird. Man erkennt in p.r = h/2p sofort die Bohrsche Quantenbedingung (für n = 1). Sie liefert eine E_kin  proportional zu 1/r² (E_kin an welcher Stelle?). Das Minimum der Gesamtenergie erhält man durch Ableitung der beiden Terme (prop. -1/r und prop. 1/r²) nach r. Das Verfahren liefert erstaunlich gut die exakte Grundzustands-Energie des H-Atoms (und ein Maß für den Atomradius).

Leider widerspricht es der Quantentheorie, insofern es explizit davon ausgeht, dass kinetische Energie und potenzielle Energie des Elektrons im Kernfeld gleichzeitig existieren. Wir wissen ja aus der QT, dass in den stationären Zuständen, also solchen mit be-stimmter Gesamtenergie E, weder kinetische noch potenzielle Energie gleichzeitig zur Gesamtenergie messbar sind und allgemein auch diese nicht untereinander gleichzeitig. Ein solches Verfahren würde mir weniger gefallen, da es ja gerade vom Ziel wegführt, einem Verständnis der QP näher zu kommen. Dass es komplementäre Größen gibt, die ein physikalisches System nicht gleichzeitig haben kann, wie hier Ort und Impuls bzw. potenzielle Energie und kinetische Energie oder kinetische und Gesamtenergie, scheint mir ein so wichtiger Gesichtspunkt zu sein, dass er nicht verletzt werden dürfte. W_pot kann nur eine abstrakte "Potenzialfunktion" sein; "Potenzialoperator" und "Operator der kinetischen Energie" müssen wir in der Schule ja mit Recht vermeiden.

Eine genauere Analyse lässt sogar Zweifel am Ansatz E_pot prop. -1/r aufkommen, weil ja der Ansatz nur für festen Radius r korrekt ist, aber hier auch noch angewandt wird, wenn r den "Aufenthaltsbereich" des Elektrons kennzeichnen soll. Man kann aber zeigen, dass die über den "Aufenthaltsbereich" mit Radius R gemittelte potenzielle Energie des Coulombpotenzials ebenfalls prop. -1/R ist, allerdings mit einem Faktor 3/2. Das hätte Konsequenzen für die quantitative Lage der Energieniveaus. Gründe für den guten "Erfolg" der originalen Rechnung sind auch klar: Die Rechnung ist identisch mit der vom Bohrschen Atommodell, wenn eine potenzielle Energie wie bei einer Kreisbahn mit Radius r im Coulombfeld angesetzt wird und die Bohrschen Quantenbedingung in der kinetischen Energie berücksichtigt wird.

Beispiel 2:

Nach einem anderen Verfahren wird das Coulombpotenzial des H-Atoms durch ein kugelsymmetrisches abschnittsweise konstantes Topfpotenzial mit unendlichen Wänden ersetzt, dessen Boden negative Energie W₀ hat. W₀ und Radius werden geeignet abgeschätzt. Dann werden die vermeintlich bekannten Energiestufen des Topfpotenzials (für unendlich tiefen Topf mit Boden bei Energie 0) zu der potenziellen Energie W₀ im Topfpotenzial-Boden addiert um eine Gleichung für die Gesamtenergie zu erhalten, zusammengesetzt aus kinetischer und potenzieller Energie. Auch hiermit können die Energiestufen überraschend gut abgeschätzt werden. Unschön im Hinblick auf ein quantenmechanisches Atommodell erscheint wieder, dass das Verfahren die Vermutung nahelegt, dass das Elektron gleichzeitig potenzielle (W₀) und kinetische Energie besitze, auch, wenn dies als allgemeine Aussage anderswo in solchen Darstellungen abgelehnt wird. (Vielleicht würden die Autoren solcher Vorgehensweisen einwenden, dass das Hinzufügen eines konstanten Potenzials W₀ ja nur eine Verschiebung des Koordinatenursprungs der Energieskala bedeutet; dann könnte man über dieses Argument reden.) Für eine Abschätzung der Energiestufen ist eine solche Vorgehensweise wohl genügend gut; zu mehr taugt sie wohl nicht. Dafür taugt aber auch das Bohrsche Modell, das aus anderen Gründen der Quantenmechanik widerspricht.

Übrigens: Man umgeht das Problem der Kugelgeometrie nur in versteckter Weise: Die Energie-Eigenwerte für die Kugelgeometrie sind auch für das einfache Topfpotenzial nur für kugelige Zustände mit Bahndrehimpuls l = 0 relativ leicht herzuleiten (Vgl. Flügge, Rechenmethoden der Quantenmechanik, 33. Aufgabe). Nur für solche Zustände gilt: E = h²/2m p²/R² n² =   h²/(8mR²) n²  (n e N) mit dem Kugelradius R. Für unterschiedliche Drehimpulsquantenzahlen l ¹ 0 erhält man sehr viel mehr weitere Zustände mit nicht analytisch angebbaren Energieformeln als Lösungen der zuständigen Besselschen Differentialgleichung.

3. Grundfakten der Quantenphysik und heuristische Prinzipien

Zunächst:  Was ist ein Teilchen? Die Quantentheorie sagt dazu nur eines: Eigenzustand des Teilchenzahloperators. In die Sprache der Schule übersetzt, könnte man sagen, dass Teilchen solche Quantenobjekte sind, die abzählbar sind. Das heißt, es kommen 0, 1, 2 oder 3, ... Objekte vor und es gibt Zählgeräte dafür. In diesem Sinn ist ein Elektron oder ein Photon per definitionem immer ein Teilchen, ohne jede Einschränkung. Genauso ein komplexes Fullerenmolekül oder ein Uran-Atom, trotz ihres komplizierten inneren Aufbaus. Wellen dagegen kann man nicht zählen. Sie sind niemals Teilchen im Sinne der Quantenphysik. Aber Licht und Materie kommen nicht nur in Teilchen-Zuständen mit einer be-stimmten Anzahl von Teilchen vor. Das ist eine der Stellen, an denen sich Abweichungen von der klassischen Vorstellung eines Teilchens ergeben. Bei geladenen Teilchen ist der (seit ca. 1930) neue Teilchenbegriff in Einklang mit dem Millikan-Versuch, der ungeteilte Elektronen ausschließt. Bei Photonen zeigt das Grangier-Experiment, dass Photonen nur ungeteilt und nur abzählbar vorkommen (Simulationsprogramm PHOTONEN vom Autor). Es gab eine Reihe von handfesten Argumenten, die nach langem Ringen um die Interpretation der Schrödinger-Theorie Anfang der dreißiger Jahre des letzten Jahrhunderts die Annahme von "verschmierten" Elektronen, Ladungswolken im Atom und konkreten Wellenpaketen endgültig widerlegten (nicht beobachtete Selbstwechselwirkung, Millikan, einigermaßen lokalisierte Wellenpakete bleiben i.a. nicht lokalisiert, sondern fließen auseinander, die Wellenfunktion stellt keine Wellen im Anschauungsraum dar, sondern Wellen in abstrakteren Konfigurationsräumen, die i.A. hochdimensional sind - bei 2 Teilchen ohne Spin schon 6-dimensional). Wellenpakete für Wahrscheinlichkeitsverteilungen sind natürlich wesentlicher Bestandteil der quantitativen Theorie.

Die Grundfakten bzw. darauf aufbauenden heuristische Prinzipien bilden ein konsistentes System. Man kann natürlich an einzelnen Punkten, insbesondere an Formulierungen, rütteln, muss dann aber darauf achten, dass wieder ein in sich geschlossenes System von Argumenten entsteht.

• A Eine Messgröße erhält erst durch eine Messung einen physikalischen Sinn. Sonst ist die Messgröße un-be-stimmt (objektive Un-be-stimmtheit), also nicht nur unbekannt, sondern die betreffende Messgröße existiert nicht als Eigenschaft des Quantensystems. I.A. ergeben sich bei der Messung streuende Messwerte, die dem objektiven Zufall unterliegen. (Wiesner/Müller: "dynamische Eigenschaft"). Damit hängen dann auch "objektive Wahrscheinlichkeiten" für das Eintreten von Messwerten zusammen.

  • Spin  (und auch V21 Spin-Messer oder Stern-Gerlach-Apparatur) : Das Experiment zeigt: Vor einer Messung hat das Teilchen keinen be-stimmten Spin. Ein zweiter gleichgerichteter Spin-Messer liefert andererseits ein reproduzierbares Messergebnis (oberste Zeile der 2. Figur).

  • Beispiel: Durchtrittsort beim Doppelspalt: Es ist vollkommen sinnlos, zu fragen, ob das Teilchen durch Spalt A oder B oder beide gleichzeitig gegangen ist, solange einer solcher Ort nicht gemessen ist. Alle Sprechweisen, in denen von "gleichzeitig durch beide Spalte" die Rede ist, sind abzulehnen, weil dabei angenommen wird, dass sich das Teilchen irgendwie aufteilt, und weil behauptet wird, der Ort existiere auch unabhängig von einer Messung.

• B Nicht alle klassisch denkbaren Eigenschaften eines Systems sind gleichzeitig realisiert/haben gleichzeitig einen physikalischen Sinn/sind gleichzeitig messbar (In diesem Sinn möchte ich Komplementarität verstehen). Beispiele: Ekin und Epot beim H-Atom oder im Potenzialkasten, Ekin und Epot beim Tunneleffekt, x und px beim Doppelspalt, beim H-Atom. Noch einmal (untere Zeile der 2. Figur):  Spin (Durch die y-Messung ist die Information über die frühere z-Messung verloren gegangen.)

  Mit Hilfe der (A) objektiven Un-be-stimmtheit und der (B) Nicht-Gleichzeitigen-Messbarkeit /Komplementartät   lassen sich viele naive Fragen als physikalisch sinnlos erkennen. Darin liegt ihr Wert für die Schule.

• C Einteilchen-Interferenz als Interferenz von nicht unterschiedenen klassisch denkbaren Möglichkeiten (Es gibt auch eine Zwei-Teilchen-Interferenz, von der hier nicht gesprochen werden soll.) Interferenz findet statt, wenn zu einem Ereignis zwei oder mehr klassisch denkbaren Möglichkeiten beitragen, zwischen denen nicht unterschieden wird.

  Diese neue Deutung der Interferenz ist eine Konsequenz aus dem bekannten Taylor-Versuch oder neuerer Varianten (Tonomura): Bereits 1 Teilchen führt danach beim Doppelspalt zur Interferenz, die allerdings erst erkennbar wird, wenn der Versuch immer wieder mit einem identisch präparierten Teilchen (demselben oder einem anderen davon ununterscheidbaren) wiederholt wird.

  Ich gehe davon aus, dass Schüler unabhängig von dieser Diskussion Interferenz bei klassischen Wellen verstanden haben (am besten lange vorher, in keinerlei Zusammenhang mit der Quantenphysik). Aber in Zusammenhang mit Interferenz in der Quantenphysik werden keine Wellen gebraucht. Deswegen lehne ich auch so abstruse Sprechweisen wie "das Elektron interferiert am Doppelspalt mit sich selbst" ab. In dieser Aussage steckt ja doch wieder die Annahme, dass es "in Wirklichkeit" einen Durchtrittsort des Elektrons gibt, dass er jetzt sogar aufgespalten ist in zwei Orte.

  Einteilchen-Interferenz als Interferenz von nicht unterschiedenen klassisch denkbaren Möglichkeiten ist ein sehr tragfähiges heuristisches Konzept, weil es sich auf alle möglichen Typen von Experimenten anwenden lässt. "Klassisch denkbare Möglichkeiten" ist eine Formulierung von Küblbeck und Müller, die ich für sehr treffend halte. Beispiele:

  • 2 klassisch denkbare Möglichkeiten von Durchtrittsorten beim Doppelspalt,
  • 2 klassisch denkbare  Möglichkeiten von Wegen durch ein Mach-Zehnder-Interferometer,
  • 2 klassisch denkbare Möglichkeiten von Impulsen beim linearen Potenzialtopf führt zu Minima und Maxima in der Nachweiswahrscheinlichkeit in Abhängigkeit vom Ort, wenn der Impulsbetrag einen geeigneten Wert hat: stationärer Zustand mit so genannten "stehenden Wellen" (die ich hier nicht erwähnen würde).
  • 2 klassisch denkbare Möglichkeiten von Energiewegen durch das Ramsey-Interferometer (Raimond, Brune, Haroche) führen zu Besetzungszahl-Maxima und -Minima bei Variation des Abstands der Ramsey-Zonen für ein bestimmtes Energieniveau.

  In allen Fällen kann man mit der "Interferenz der Möglichkeiten" Maxima und Minima qualitativ erklären. Es wird also nicht behauptet, dass hier irgend "etwas" interferiert, wie etwa zwei Wellen, die sich Schüler höchstwahrscheinlich materiell vorstellen, sondern viel abstrakter: "Möglichkeiten". Verfahren, wie die "Interferenz von Möglichkeiten" quantitativ durchgeführt werden sollte, überschreiten höchstwahrscheinlich den Rahmen der Schulphysik. Addition von Wellenfunktionen (wie Sie es vielleicht von Feynman kennen), Zeigern (als vereinfachte Variante von Pfadintegralen, ebenfalls popularisiert von Feynman), etc. werden aber für die Schulphysik diskutiert. Es gibt eine Reihe von Simulationsprogrammen dafür, z.B. von Bader, deren Technik m.E. für die Schulphysik weniger interessant ist, sehr aufschlussreich aber viele ihrer Ergebnisse.

• D WWI und Interferenz sind komplementär zueinander (Küblbeck und Müller nennen das allein - wie mir scheint - Komplementarität, obwohl Komplementarität (gemäß B) eher allgemeiner erscheint.

  Zugrunde liegen zwei verschiedene Experimente: (Denken Sie meinetwegen an einen Doppelspalt-Versuch oder ein Mach-Zehnder-Interferometer.)

  • In dem einen Experiment wird gefragt, wie sich ein System zeigt, wenn zwischen zwei oder mehr klassisch denkbaren Möglichkeiten nicht unterschieden wird. Das ist ein typisches Interferenz-Experiment.
  • In dem anderen Experiment wird gefragt, auf welchem Weg Teilchen die Apparatur durchlaufen. Dann wird WWI gewonnen (Welcher-Weg-Information).

  Zu den zwei Typen von Fragestellungen gehören offenbar als Erfahrungstatsache - Zeilinger leitet aber auch das aus der Nicht-Gleichzeitigen-Messbarkeit her -  völlig unterschiedliche Antworten der Natur, die sich nicht miteinander vereinbaren lassen, die eben komplementär sind. Beispiele. Unterschiedliche Reaktion des Systems.

  Das hat nichts mit einem angeblichen "Wellen-" oder "Teilchencharakter" zu tun ( c) (obwohl manche das als eine bequeme Sprechweise, wie ein mündliches Stenogramm, ansehen). Fragen, "ob ein Quantenobjekt als Teilchen auf einem bestimmten Weg oder als Welle auf zwei Wegen gleichzeitig eine Apparatur durchläuft", sind abstrus und dürfen nicht wörtlich genommen werden. Beispiele dazu sind einige Anordnungen (z.B. ein MZI) "mit verzögerter Entscheidung", wo sich der Experimentator erst verspätet entscheidet, ob er ein WWE oder ein Interferenz-Experiment durchführen möchte. Diese Entscheidung fällt erst dann, wenn das Quantenteilchen die Apparatur weitgehend "durchlaufen" hat oder gar schon nachgewiesen ist. Auch mit Quanten-Auslöschern (Quanten-Radierern) kann WWI oder Interferenz nachträglich den Messdaten entnommen werden, aber jede nur für sich. Dabei wäre es besonders abstrus, anzunehmen, dass sich das Teilchen erst nach dieser Auswertung entscheiden würde gemäß seinem vermeintlichen "Wellencharakter" oder seinem vermeintlichen "Teilchencharakter" lange vorher die Apparatur durchlaufen zu haben.

  a) Wheelersches Gravitationslinsen-Interferometer  Vor einem eventuellen WWE  fällt der Experimentator keinerlei Entscheidung über einen vermeintlichen "Weg", auch, wenn dieser nach klassischer Vorstellung Milliarden Jahre vorher eingetreten sein müsste. Wäre auch absurd, wenn sich die Photonen bei der Entscheidung des Experimentators über die Art des Experiments zur Jetztzeit rückwärts entschließen müssten, sich als Wellen (beide Wege gleichzeitig) oder aber als Teilchen (bestimmter Weg) zu "verhalten". Es gibt kein "Verhalten" von Quantenobjekten, nur Antworten auf Fragen des Experimentators.

  b) .Mach-Zehnder-Interferometer mit verzögerter Entscheidung (Prinzip)  !!!! keine Entscheidung über einen "Wellen-" oder "Teilchencharakter"

  c) Mach-Zehnder-Interferometer mit verzögerter Entscheidung (Realisierung)  !!!! keine Entscheidung über einen "Wellen-" oder "Teilchencharakter"

• E HUR (= Heisenbergsche Un-be-stimmtheitsrelation) Sie ist eine direkte Folge der Nicht-Gleichzeitigen-Messbarkeit / Komplementarität zweier physikalischer Größen (Ausnahme: Energie-Zeit-Unschärfe).

  Sie besagt Folgendes: Ein Quanten-System sei in einem bestimmten Zustand präpariert worden. Wenn für diesen Zustand A und B zwei nicht gleichzeitig messbare Größen sind, also, wenn das System die beiden Messgrößen nicht gleichzeitig als Eigenschaften hat, dann ist mindestens eine der beiden Größen un-be-stimmt, häufig auch beide. Aber innerhalb bestimmter Bereiche, innerhalb der Un-be-stimmtheiten DA und DB. (d.h. A und B existieren in diesem Zustand nicht als exakte Eigenschaften des Systems) werden zukünftige Messwerte von A und B  für den Zustand doch so realisiert werden, dass sie nur innerhalb der Un-be-stimmtheiten streuen. Ihr Produkt lässt sich nicht unter eine bestimmte Schwelle drücken.

  Wichtig:

  • Die beiden Messgrößen A und B können nicht gleichzeitig als Eigenschaften des Systems existieren (sind nicht gleichzeitig messbar).
  • Die Un-be-stimmtheiten geben nicht den Schwankungsbereich tatsächlich existierender Eigenschaften oder die Bereiche der Unkenntnis ("Ungewissheit") dieser Eigenschaften an, sondern die Bereiche, innerhalb deren die Eigenschaften höchstens einen ungefähren physikalischen Sinn haben, innerhalb deren die Eigenschaften bei künftigen Messungen realisiert werden werden.
  • Beispiele für A und B sind nicht nur Orts- und gleichgerichtete Impulskoordinate, sondern auch E_x und B_x, oder E_x und E_y bei elektromagnetischen Wellen, verschieden orientierte Drehimpulskomponenten oder Teilchenzahl/Amplitude und Phase bei einer elektromagnetischen Welle oder Schallwelle, Gesamtenergie und kinetische Energie im Atom, kinetische und potenzielle Energie im Atom, Gesamtenergie und Ort.

  M.E. stellt die HUR keine Einschränkung unserer Kenntnis dar, sondern eine Erweiterung, weil ja mindestens eine der beteiligten Messgrößen un-be-stimmt ist, also vor der Messung nicht Eigenschaft des Systems ist. Dass die späteren Messwerte dennoch  im wesentlichen "nur" innerhalb der Un-be-stimmtheiten streuen werden, ist ein "Geschenk der Quantenphysik an den Physiker, der weiterhin noch ein bisschen klassisch denken möchte".

  Weil Un-be-stimmtheiten in der klassischen Physik nicht vorkommen (höchstens Bereiche der Unkenntnis oder Schwankungsbereiche, häufig Unschärfen oder Ungewissheiten genannt), kann die HUR auch nicht mit klassischen Methoden, also z.B. in der Schulphysik, hergeleitet werden.  Die HUR ist nicht eine Folge unkontrollierbarer mechanischer Stöße, wie manchmal behauptet wird ("Heisenberg-Mikroskop"). Solche Argumente setzen letzten Endes voraus, dass es ein ungestörtes Verhalten in Wirklichkeit gebe, das wir nur nicht kennen. Bei Herleitungen in der Schule muss man also sehr vorsichtig sein. Solche anschaulichen Herleitungen kranken oft daran, dass bei ihnen Dx bzw. Dp_x Schwankungsbereiche oder Unsicherheitsbereiche von an sich existierenden, nur unbekannten Messgrößen sind. Benutzt man eine solche "Herleitung" in der Schule, suggeriert man unvermeidlich, dass die Schüler Un-be-stimmtheiten mit Schwankungsbereichen oder Bereichen der Unkenntnis an sich existierender Eigenschaften verwechseln. Deshalb sollte man m.E. so die HUR an der Schule nicht "herleiten", sondern mehr anwenden. Es gibt halbklassische Herleitungen, z.B. die HUR beim Doppelspalt, bei denen der Charakter der Un-be-stimmtheiten besser, aber auch nicht ganz befriedigend herauskommt.

  Beispiel einer krummen "Herleitung": klassisches Bohrsches H-Atom

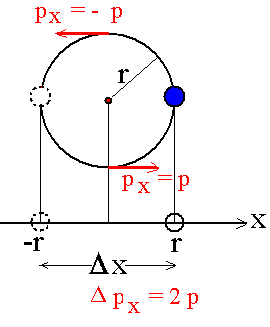  Es gilt die Quantenbedingung:  p.r = n.h/2p  (n e N). Geht man davon aus, dass die x-Koordinate schwankt zwischen -r und r, und die x-Koordinate des Impulses px  zwischen  -p und p, dann sind die Schwankungsbereiche Dx » 2r und Dpx » 2p, also  Dx.Dpx » 4.r.p = 2 n.h/p . Bei geeigneter Wortwahl würde man auch noch ein >-Zeichen hineinmogeln können. Man hat eine Gleichung erhalten, die wie eine HUR aussieht, aber keine ist: Dx und Dpx sind nicht die quantenphysikalischen Un-be-stimmtheiten, sondern Schwankungsbereiche. Ich meine, eine solche "Herleitung" hätte für die Schule den einzigen Sinn zu zeigen, was die HUR nicht ist.

  Beispiel einer halbklassischen Herleitung: Doppelspalt:

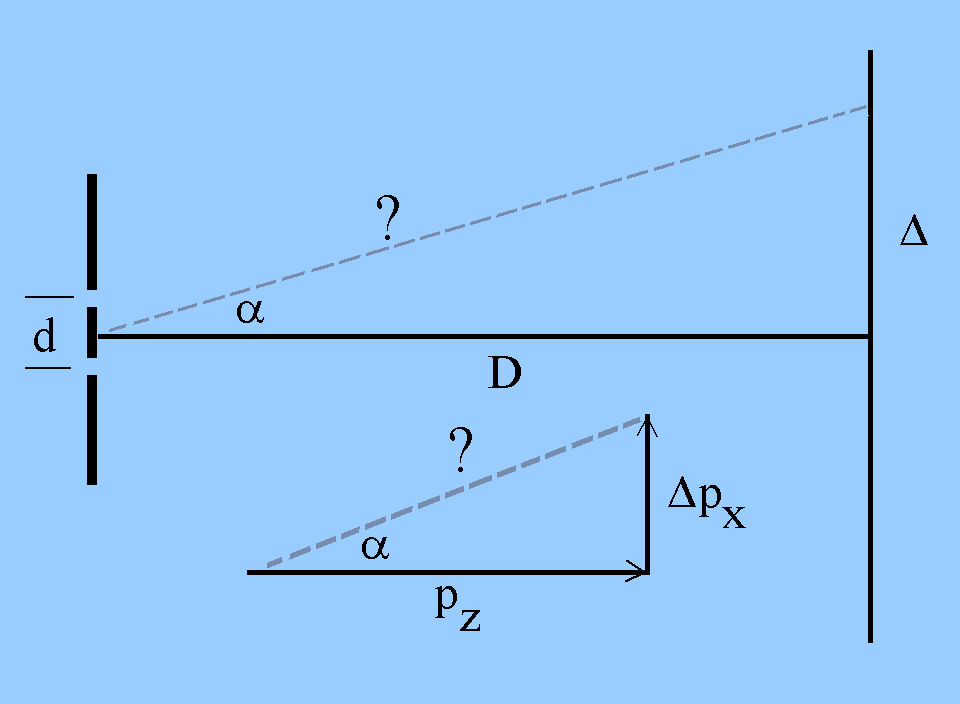  Der Spaltabstand d kann als Maß für die Un-be-stimmtheit genommen werden. Die Impuls-un-be-stimmtheit wird aus der Interferenzfigur abgeschätzt, wenn angenommen wird, dass die "Seitwärtsstreuung" der Messwerte für den Ort durch eine Streuung des Impulses in Querrichtung zustandekommt ( wenn angenommen wird, dass die seitliche Streuung auf dem Schirm eine Folge der Un-be-stimmtheit des Querimpulses ist). Man sollte m.E. den Eindruck vermeiden, dass die seitliche Streuung auf dem Schirm die ursächliche Folge eines Querimpulses sei, den das Teilchen bei einer Wechselwirkung mit den Atomen des Doppelspalts erhalten habe. Eine solche Behauptung wäre m.E. in einem nicht tolerierbaren Widerspruch zur Quantentheorie. Problematisch erscheint es auch, dass es so aussieht, als bewege sich das Teilchen vom Doppelspalt zum Nachweisort längs einer Bahn mit dem Ablenkwinkel a. Deswegen fasse ich die gestrichelte Strecke als Peillinie auf.

  Ich meine, statt die HUR im Schulunterricht "herzuleiten" sollten mehr Anwendungen und Konsequenzen diskutiert werden. Manche Probleme kann man aber auch hier nicht vermeiden.

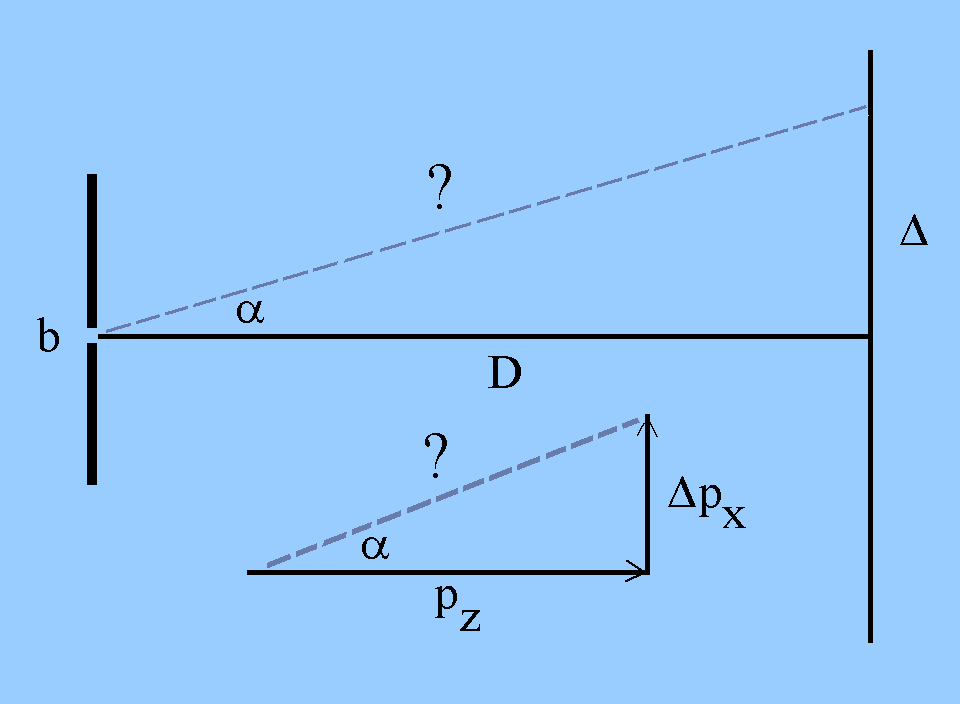  Beispiel einer Anwendung: Einfachspalt Durch die Spaltbreite b ist der Ort un-be-stimmt innerhalb des Bereichs Dx = b (oder b/2). Daraus ergibt sich gemäß der HUR eine Impuls-un-be-stimmtheit für die gleiche Koordinatenrichtung Dpx >= h/4pb. Die Impuls-un-be-stimmtheit führt zu Streuungen des Nachweisorts in einem Bereich gemäß D/D = Dpx/pz, also D = D h/4pb / (h/l) = D l / 4pb, wobei die deBroglie-Wellenlänge eingesetzt wurde. Wenn das aufgefasst wird als die (halbe) Breite des zentralen Maximums, kann man folgern, dass das zentrale Maximum um so breiter ist, je schmaler die Spaltbreite und je größer die Wellenlänge. Das ist die Erkenntnis, die man aus der Anwendung der HUR gewinnen kann, sie ist zweifellos richtig. Zum Vergleich: Die Wellentheorie des Einfachspalts lehrt für die Lage des 1. Minimums in Kleinwinkelnäherung: l/b = D/D, also D = D l/b. Der zusätzliche Faktor 1 / 4p ist reine Willkür und ließe sich jederzeit anders abschätzen.

Das nachfolgende Grundfaktum sollte nur der Lehrer im Hinterkopf behalten, es sollte seine Sprechweisen bestimmen, aber nicht die Inhalte des Unterrichts:

F Revision des Teilchenbegriffs und des Wellenbegriffs bei Vielteilchen-Zuständen Einerseits gibt es keinen "Welle-Teilchen-Dualismus", da Teilchen klar definiert und ohne "Alternativcharakter" sind. Elektronen und Photonen sind unzweifelhaft Teilchen im Sinne der Quantenphysik, weil sie abzählbar sind. Teilchen sind keine Wellenpakete, es gibt keine "verschmierten Teilchen"; auch im Atom sind Elektronen keine stehenden Wellen. Wellenpakete können aber dazu taugen, die wahrscheinlichen Nachweisorte eines Teilchens zu beschreiben, wenn dieses im Ortsraum (oder auch im Impulsraum) wenigstens einigermaßen lokalisiert ist.

Der Teilchenbegriff hat nichts mit Lokalisierung zu tun. Ein Teilchen, das im Impulsraum scharf lokalisiert ist (enges Wellenpaket zur Beschreibung von Messungen an ihm), ist im Ortsraum total unlokalisiert und umgekehrt. Andererseits handelt es sich bei Quantenteilchen nicht um klassische Teilchen, denn:

• ein Quantenteilchen besitzt nicht eine klassisch denkbare Eigenschaft ohne eine Messung und nie sind alle klassisch denkbaren Eigenschaften gleichzeitig realisiert: "Ein Teilchen besitzt nicht alle klassisch denkbaren Eigenschaften gleichzeitig", also hat z.B. nicht gleichzeitig Ort und Geschwindigkeit. M.E. sind diese beiden Grundfakten der Schlüssel zum Verständnis der QP.

• in Mehrteilchenzuständen (also z.B. einem Photonen-Zwilling, oder einem He-Atom mit zwei Elektronen oder anderen Mehrelektronen-Atomen) liegen keine individuellen Teilchen vor. Mehrteilchenzustände (verschränkte Zustände) sind keine "kombinierten" Einteilchenzustände. Physikalisch real ist nur der Gesamtzustand. Erst durch eine Messung wird er aufgebrochen in individuelle Teilchen, erhalten diese Teilchen dann individuelle Eigenschaften, aber so, dass die Eigenschaften des Gesamtsystems bewahrt bleiben (Folge von Erhaltungssätzen).
  • (EPR Vorschlag von Clauser-Horne-Holt-Shimony 1969, ausgeführt von Freedman und Clauser u.a.1972 : Nachweis der Korrelation der individuellen Eigenschaften beider Teilchen nach einer Messung; ohne eine Messung haben die Teilchen keine Individualität. Analogie zu Doppelspaltversuch: Es gibt keinen individuellen Durchtrittsort ohne seine Messung.
  • Aspect: Nachweis der Korrelation der individuellen Eigenschaften beider Teilchen nach einer Messung: noch raffinierter. Schließt "lokal realistische Theorien" aus.
  • G75 Bertlmanns Socke: individuelle Eigenschaften der beitragenden Teilchen sind nicht nur ungewiss, wie bei Bertlmanns Socke, sondern un-be-stimmt, d.h. sie existieren nicht als Eigenschaften ohne eine Messung.
  •  Stern-Gerlach: Nachweis anhand des Spins, dass individuelle Eigenschaften der beitragenden Teilchen  vor einer Messung nicht nur ungewiss, sondern un-be-stimmt sind.

• nicht alle Materie kommt in Zuständen mit be-stimmter Teilchenzahl vor. Ein Zustand mit be-stimmter Teilchenzahl  wird Teilchenzustand oder Fock-Zustand genannt. Der Gegensatz dazu ist nicht etwa ein "Wellenzustand" (was immer das heißen sollte), sondern ein Zustand mit un-be-stimmter Teilchenzahl. Das ist allerdings eine sehr fernliegende Vorstellung und spielte bis 1963 quasi keine Rolle.
  • Erst seit 1963 (Glauber, Nobelpreis dafür 2005) sieht man hier weiter: eine klassische Lasermode ist eine Näherung für etwas, was sich quantenphysikalisch als Folge eines Zustands mit un-be-stimmter Photonenzahl darstellen lässt. Das heißt: Die Teilchenzahl (Photonenzahl), die ein Maß für die gemessene Amplitude ist,  ist keine Eigenschaft eines solchen kohärenten Zustands. Misst man die Photonenzahl jeweils in einer jeweils gleich präparierten Lasermode eine bestimmte Zeit lang, erhält man streuende Messwerte, die einer Poisson-Verteilung gehorchen, typisch für einen solchen Zustand. Der Erwartungswert der elektrischen Feldstärke bzgl. eines solchen kohärenten Zustands genügt genau der Gesetzmäßigkeit einer klassischen Welle. Erinnerung an zugehörige HUR mit Phasen- und Amplituden/Teilchenzahl-Un-be-stimmtheit: Bei großer mittlerer Teilchenzahl ist sowohl die relative Amplitude als auch die Phase quasi scharf, wie bei einer klassischen Welle.

  • Ähnlich: Atomlaser. Erzeugung des Atomlasers. Atomzahl un-be-stimmt (Koehl et. al. 2005: Nachweis der Poisson-Verteilung im BEC-Zustand, der Bose-Einstein-Verteilung im thermischen Zustand).  "Un-be-stimmte Teilchenzahl" bedeutet nicht Erzeugung und Vernichtung von Atomen, sondern im Grundzustand ist die Atomzahl un-be-stimmt, auch nicht Schwankungen an sich fester Teilchenzahlen, sondern: die Teilchenzahl ist keine Eigenschaft des Systems.

  • Bei einem Atomlaser aus bosonischen Atomen liegen etwas andere Verhältnisse als bei einem Laser vor, weil die Atome in ihm wechselwirken. Dennoch gibt es eine berechtigte Vermutung, dass auch hier ein kohärenter Zustand mit un-be-stimmter Atomzahl vorliegt: Die Atomzahl in diesem Zustand ist nicht Eigenschaft des Systems. Seit 2005 ist nachgewiesen (Züricher Gruppe um Koehl, Esslinger und Pariser Gruppe um Westbrooke), dass sich bei der Messung der Atomzahl in einem solchen Zustand streuende Messwerte ergeben, die einer Poisson-Verteilung genügen, wie bei einem Lichtlaser. Mit dem kohärenten Zustand des Atomlasers hängt es zusammen, dass sich dieser nun wirklich wie eine makroskopische Materiewelle verhält; zwei Atomlaser interferieren und geben eine Interferenzfigur, deren Maxima und Minima z.B. durch Schattenwurf nachweisbar sind. Der Erwartungswert der "Feldstärke" entspricht einer klassischen, wenn auch komplexwertigen Welle im Anschauungsraum. Sein (Betrags-)Quadrat ist proportional zur Zahl der Teilchen, die in einem Intervall der Breite Dx nachgewiesen werden.

  • Es gibt auch  kohärente Phononenzustände: klassische Schallwellen (Nägerl/Blatt , Innsbruck, Video), und seit 2006 sind auch kohärente Polaritonen (Cavalleri, Oxford) sichtbar gemacht worden, also Zustände mit un-be-stimmter Phononen und Polaritonenzahl. Phononen und Polaritonen sind allerdings Quasi-Teilchenzahl.

4. Anwendungen der heuristischen Methoden in der Schule

1. Deutung der Interferenz beim Doppelspalt: zwei klassisch denkbare Möglichkeiten für den Durchtrittsort ("Einteilchen-Interferenz") => Interferenz mit der Ausbildung von Maxima und Minima. Abzulehnende Sprechweise: "Das Elektron interferiert am Doppelspalt mit sich selbst": würde Existenz eines bzw. zweier Durchtrittsorte suggerieren. Wird ein Durchtrittsort gemessen, d.h. wird Welcher-Weg-Information (WWI) gewonnen, dann verschwindet die Interferenz. Bei ungenauer WWI wird die Interferenz verwaschen. (Sonderfall der Komplementarität)

2. Scully-Englert-Walther-Experiment:  Die Störung der Interferenz durch ein Welcher-Weg-Experiment (WWE) hat nichts mit einer klassischen Störung durch die Ortsmessung zu tun (in dem Sinne, dass durch die Ortsmessung unkontrollierbar Impuls an das zu messende Teilchen übertragen wird, der es sozusagen aus der Bahn schlägt und so die Interferenz verhindert), wohl aber damit, dass durch die Ortsmessung i.A. der Zustand des Systems verändert wird, in dem Sinn, dass eine vorher un-be-stimmte Messgröße jetzt be-stimmt wird. Auch bei diesem Experiment wird es offenbar: Es handelt sich um keine realistischen Wellen, sondern Wellen in einem 6-dimensionalen Raum; nur der atomare Anteil überlagert sich auf dem Interferenzschirm, während der photonische Anteil getrennt in den beiden Resonatoren zurückbleibt und nicht interferieren kann. (Sonderfall der Komplementarität, begründbar durch Wellenfunktionen im 6-dimensionalen Raum)

3. Tunneleffekt: Die klassische Argumentation ist nicht gültig, weil im Potenzialtopf Gesamtenergie und potentielle Energie oder Gesamtenergie und kinetische Energie oder kinetische und potenzielle Energie nicht gleichzeitig messbar sind, nicht gleichzeitig einen physikalischen Sinn haben. Damit ist es nicht mehr verboten, dass ein Teilchen auch in einer Potenzialbarriere zu finden ist. Ein zweites Argument, nach dem mit Hilfe der HUR stark streuende Messwerte für die (ohne Messung nicht existente) kinetische Energie sogar jenseits der Gesamtenergie zulässig ist, unterstützt das Argument. Der Tunneleffekt ist damit qualitativ erklärt. Was noch fehlt sind Wahrscheinlichkeiten für den Nachweis des Teilchens in "erlaubten" und vermeintlich "verbotenen" Potenzialbereichen. Das erfordert z.B. eine Lösung der Schrödinger-Gleichung, die m.E. auch bei anderer Vorgehensweise Schulniveau überschreitet.

4. Potenzialkasten : zwei klassisch denkbare Möglichkeiten für den Impuls => Interferenz, die zur Ausbildung von Maxima führt. (Vgl. Wahrscheinlichkeitsdichte für Nachweis eines Teilchens in der Nähe eines bestimmten Ortes. Entsprechend  gibt es auch im Atom konkurrierende klassisch denkbare Möglichkeiten, zwischen denen nicht unterschieden wird, z.B. eine radiale Auswärts- und eine radiale Einwärtsbewegung. Die Folge ist Interferenz mit Maxima und Minima längs der komplementären Größe, dem Radius. Das klingt nach stehenden Wellen. Die würde ich hier aber unbedingt vermeiden, weil m.E. die Schüler dann nicht vermeiden könnten an aus dem Zentrum quellenden und sich zum Zentrum hin kontrahierenden (realen) Wellen zu denken. Ich sehe das Grundfaktum "Interferenz als Konkurrenz nicht unterschiedener klassisch denkbarer Möglichkeiten" als eine hinreichende qualitative Erklärung von Minima und Maxima der Wellenfunktion bzw. der Nachweiswahrscheinlichkeit an.

5. Mach-Zehnder-Interferometer und Knallertest: Jeweils Demonstration, dass WWI und Interferenz sich gegenseitig ausschließen (Sonderfall der Komplementarität). Knallertest als prinzipielles Beispiel einer "nicht verbrauchenden Messung" (quantum non demolition measurement).

6. Quantenschwebungen / Ramsey-Interferometer: Entspricht Mach-Zehnder-Interferometer ("Interferenz als Konkurrenz nicht unterschiedener klassisch denkbarer Möglichkeiten"), aber statt klassisch denkbarer Wege im Ortsraum hier "Energiewege".

7. WWI-Experimente: Doppelspalt, MZI, ... Versuche mit verzögerter Entscheidung: Es wird erst entschieden, ob nach einem Weg oder nach Interferenzerscheinungen gefragt werden soll, "wenn das Teilchen die Apparat überwiegend oder ganz durchlaufen hat". Der unterschiedliche Ausgang der Experimente hat offenbar nichts mit einem vermeintlichen Wellen- oder Teilchen-"Charakter" der Teilchen zu tun, sondern mit der Fragestellung, die der Experimentator an sie richtet. Es wäre absurd zu behaupten, dass diese Entscheidung des Experimentators sich auf die Vergangenheit auswirken könnte, so dass ein Teilchen rückwärts eventuell vor Milliarden von Jahren entschieden hätte, ob es "wie ein Teilchen auf einem be-stimmten Weg, oder wie eine Welle auf zwei Wegen gleichzeitig" zum Nachweispunkt läuft. Das hat nichts mit einem vermeintlichen "Wellen-" oder "Teilchen-Charakter" zu tun!

   Beispiele dazu und vor allem Wheelers Gravitationslinsen Interferometer   v20.html

   • v19.html   Mach-Zehnder-Interferometer: Prinzip

   • v19a.html   Mach-Zehnder-Interferometer: Ausführung mit Pockelszelle

8. Quantenauslöscher:  v15a.html :  Interferenz kann auch  nachträglich noch zurückgewonnen werden, wenn Welcher-Weg-Information ausgelöscht wird. Wieder ist es so, dass die Beobachtungen nichts mit einem "Wellencharakter" oder "Teilchencharakter" zu tun haben, in dem Sinn etwa, dass einerseits "Interferenz - auf beiden Wegen gleichzeitig - Wellencharakter" und andererseits "keine Interferenz - auf  einem bestimmten Weg - Teilchencharakter" zusammengebracht werden. Die Entscheidung, ob Interferenz zurückgewonnen und WWI ausgelöscht wird, fällt ja erst dann, wenn die Photonen die Apparatur längst durchlaufen haben. Bildlich gesprochen können sie am ersten Strahlteiler ja nicht "wissen", wie sie die Apparatur nach Meinung des Experimentators durchlaufen sollen um der gewünschten experimentellen Situation zu genügen.

Liste der heuristischen Verfahren:

A objektive Un-be-stimmtheit: Eine Messgröße erhält erst durch eine Messung einen physikalischen Sinn. Sonst ist die Messgröße un-be-stimmt. B Komplementarität (Nicht-Gleichzeitige-Messbarkeit): Nicht alle klassisch denkbaren Eigenschaften eines Systems sind gleichzeitig realisiert / haben gleichzeitig einen physikalischen Sinn / sind gleichzeitig messbar. C Einteilchen-Interferenz ist die Interferenz von nicht unterschiedenen klassisch denkbaren Möglichkeiten. D WWI und Interferenz  sind komplementär E HUR als Folge der Nicht-Gleichzeitigen-Messbarkeit

Erfolge:

• keine inneren Widersprüche (wie beim überholten Welle-Teilchen-Dualismus),
• Wesentliches der QP kommt besser heraus, insbesondere durch das Herausstellen der (objektiven) Un-be-stimmtheit,
• Entlastung der Schulphysik durch weitgehenden Verzicht auf Wellenformalismen und doch
• Verständnis grundlegender Prinzipien und moderner Experimente

Eine Reihe von Fragestellungen werden als physikalisch sinnlos erkannt:

• Wie kommt ein Elektron von der Quelle zum Nachweisort?
• Wie "verhält sich" ein Elektron beim Durchtritt durch einen Doppelspalt?
• Wie "verhält sich" ein Elektron im MZI, als Welle oder als Teilchen?
• Wo hält sich ein Elektron auf, wenn man seinen Ort nicht gemessen hat?
• Wie schnell bewegt sich ein Elektron, wenn man seine Geschwindigkeit nicht gemessen hat?
• Ist ein Elektron ein Teilchen oder eine Welle?
• Wie kommt ein Elektron im linearen Potenzialkasten über einen Knoten hinweg, wenn es sich dort "nicht aufhalten" darf?

6. Eine Auswahl von Literatur und Links:

J. Küblbeck, R. Müller, Die Wesenszüge der Quantenphysik, Aulis Verlag Deubner, Köln, 2003

E. Fick, Einführung in die Grundlagen der Quantentheorie, Akademische Verlagsgesellschaft, Frankfurt am Main, 1972   (Begriffliches sehr klar!)

J.J. Sakurai, Modern quantum mechanics, Addison-Wesley, Redwood City, 1985

M. Le Bellac, Quantum Physics, Cambridge University Press, Cambridge, 2006   (auch mit moderneren Experimenten!)

A. Zeilinger, Einsteins Schleier, Die neue Welt der Quantenphysik, Beck, München, 2003  (ohne Formalismen; Begriffliches an modernen Experimenten sehr klar dargelegt)

R. Loudon, The quantum theory of light, Clarendon Press, Oxford, 2000   (kohärente Zustände von Licht)

Münchner Internetprojekt zur Lehrerfortbildung in Quantenmechanik (Milq) http://www.cip.physik.uni-muenchen.de/~milq/info/index1p01.html

http://www.forphys.de   (Enthält meine Ausführungen noch ausführlicher und noch Vieles mehr.)