Würzburger Quantenphysik- Konzept

G90 Thermische Verteilungen

Be-stimmt / Un-be-stimmt Heisenbergsche Un-be-stimmtheitsrelation

Lehrtext/Inhalt Glossar  wissenschaftliche Experimente

Im- pres- sum

Wenn ein Gas im thermischen Gleichgewicht ist, besitzt es eine Temperatur T. Je nachdem, ob die Gasteilchen Masse haben oder nicht, relativistisch sind oder auch nicht, ob sie klassisch behandelt werden können oder quantentheoretisch, im letzteren Fall auch, ob die Teilchen Bosonen oder Fermionen sind, genügen dann seine Energien bzw. Beträge der Geschwindigkeiten bestimmten Verteilungen.

• Klassisches nichtrelativistisches Gas (Maxwell-Verteilung)
• Photonengas (Plancksches Strahlungsgesetz für Strahlung schwarzer Körper)
• Bosonisches Quantengas (Bose-Einstein-Verteilung)
• Fermionisches Quantengas (Fermi-Einstein-Verteilung)

Für Interferenz-Experimente braucht man Teilchen mit möglichst einheitlicher Energie (möglichst monochromatische Teilchen). Das scheint im Widerspruch zu stehen zu den breiten thermischen Verteilungen. Hier sind weitgehend alle Energien beteiligt.

Methoden zur Gewinnung von Teilchen möglichst einheitlicher Energie werden unten diskutiert.

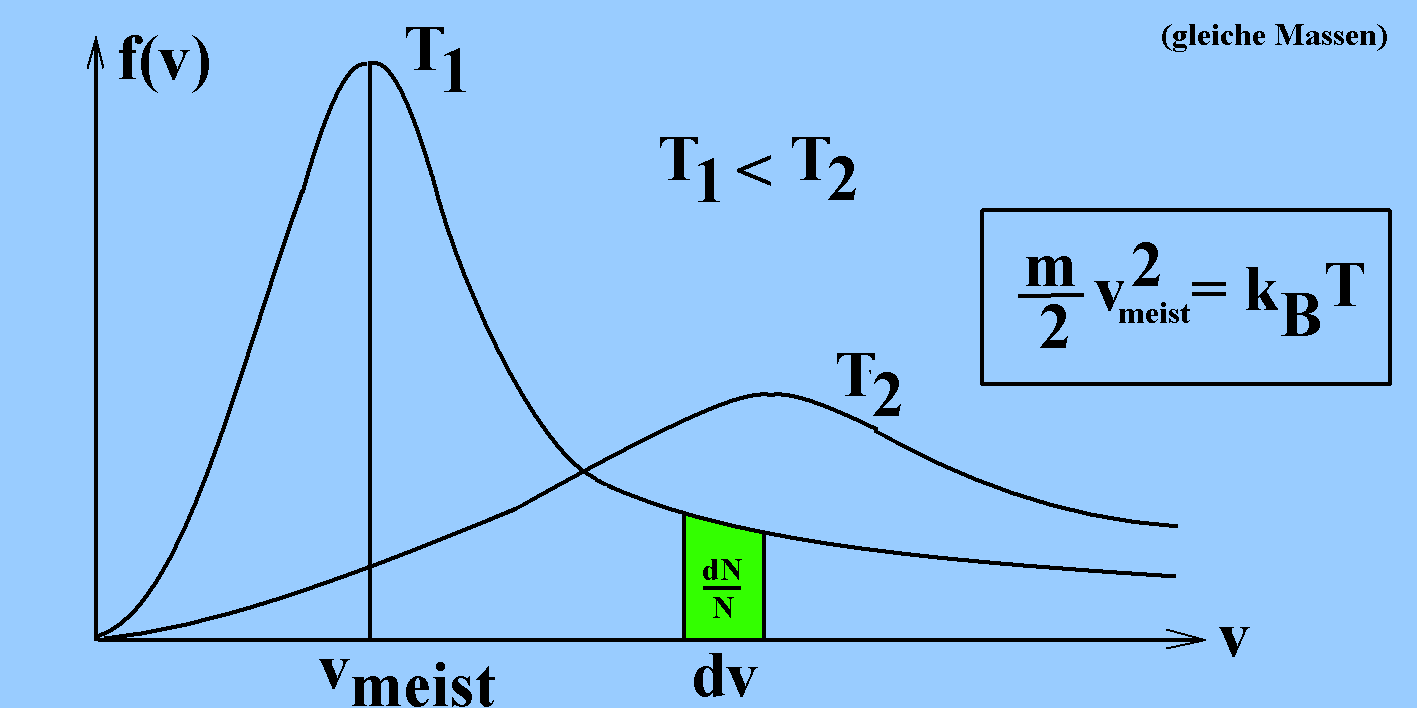
Wenn v der Betrag der Geschwindigkeit der Teilchen des nichtrelativistischen Gases ist, E ihre kinetische Energie und N ihre Gesamtzahl, gilt für die die Anzahl der Teilchen dN im Geschwindigkeitsintervall der Breite dv um v (grün markiert, bis auf Faktor N):

dN = N · f(v)·dv, wobei f(v) = 4π (m/2π kBT)3/2   v2 e -E/kBT ,   mit E = m/2 v2   Man muss sehr genau darauf achten, von welcher Variablen die Verteilung abhängen soll (v oder E?). Eine Umrechnung ist leicht möglich: Wegen dE = m v . dv gilt dann für die Zahl der Teilchen im Energieintervall dE: dN = N·f(v) / (m·v) dE    ,  also f(v)/(m·v) = 4π (1/2πkBT)3/2  √(2E) e -E/kBT Je nach Teilchenmasse und absoluter Temperatur T verlaufen die Funktionen f(v) unterschiedlich. Es gibt eine häufigste Geschwindigkeit vmeist (in der Regel wahrscheinlichste Geschwindigkeit vw genannt), für die gilt

Die so genannte mittlere Geschwindigkeit ist davon leicht verschieden: v_m = √(4/π) v_meist = 1,13·v_meist

(Eigentlich handelt es sich in diesem Zusammenhang nie um Geschwindigkeit, sondern immer um "Tempo". Die mittlere Geschwindigkeit im strengen Sinn ist natürlich bei einem klassischen Gas 0: zu jeder positiven Geschwindigkeit gibt es eine negative gleichen Betrags.)

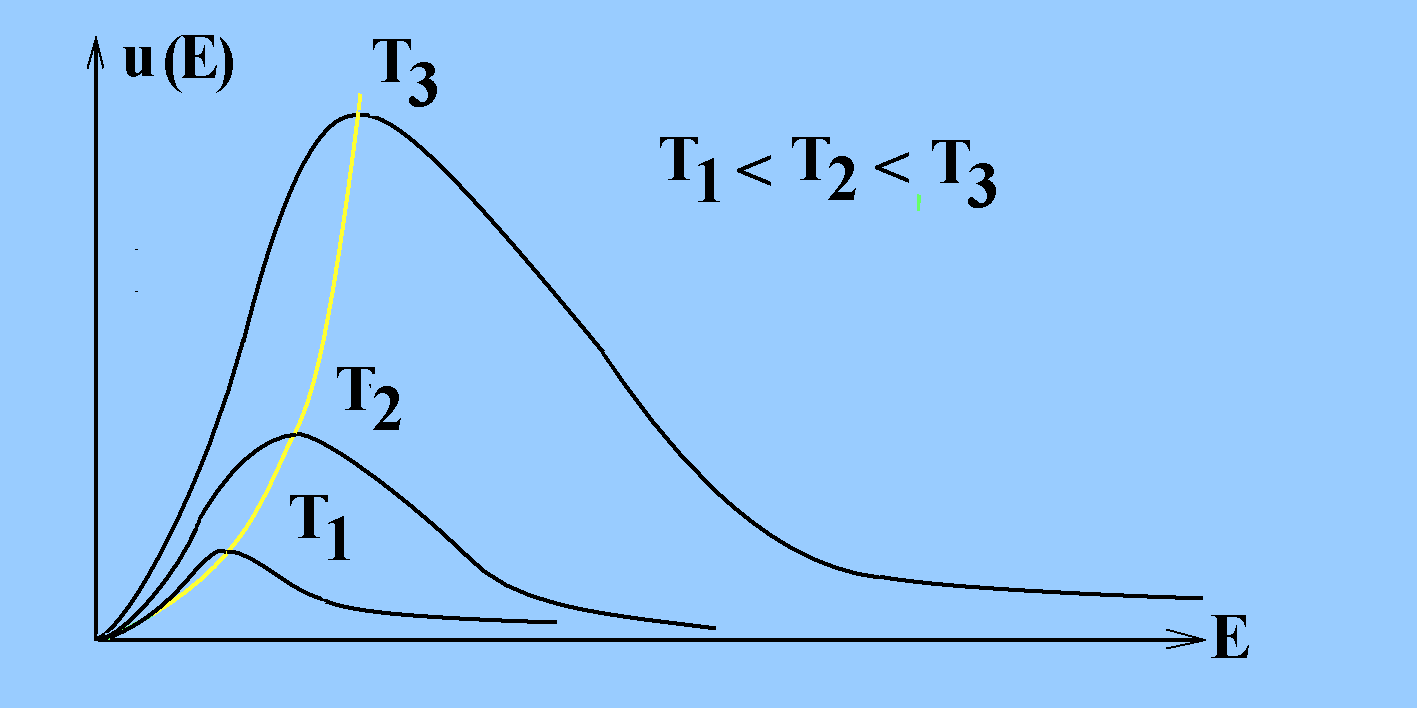
Bei der absoluten Temperatur T eines Photonengases in einem evakuierten Hohlraum gilt für die (Strahlungs-)Energiedichte du = u(E)dE der Photonen mit einer Energie E im Energieintervall dE:

du = u(E) dE , und mit E = h·f :         u(E) = 2/(hc)2 E3 ( e E/kBT - 1 )-1   wegen dE = h·df  kommt man durch Multiplikation von u(E) mit h zur Energiedichte der Photonen mit Frequenz f im Frequenzintervall df. Wegen f = c/λ   erhält man df =  c/λ2·dλ (bis auf das Vorzeichen) und die Energiedichte der Photonen mit einer Wellenlänge im Wellenlängenintervall dl um λ ist: du =   hc/λ2 · u(E) · dλ     wobei E zu ersetzen ist durch E = h·f = hc/λ Im letzten Fall tritt ein Maximum auf bei einer bestimmten Wellenlänge λmeist = b/T   b = 2,8978·10-3 m·K (Wiensches Verschiebungsgesetz: die Maxima liegen auf der gelben Kurve) Integriert man über alle Energien (Frequenzen, Wellenlängen), so erhält man die totale Energiedichte u = s·T4, also das Stefan-Boltzmannsche Gesetz mit s = 5,67·10-8 W/m2·K4.

Wie kann man Teilchen mit weitgehend einheitlicher Energie erhalten?

• Bei einem klassischen nichtrelativistischen Gas mit Maxwell-Verteilung haben die am häufigsten vorkommenden Teilchen eine Energie E_meist = k_B·T mit der Boltzmann-Konstanten k_B = 1,38·10^-23 J/K = 8,6·10^-5 eV/K. Ihre Energie ist also durch die absolute Temperatur bestimmt. Weil aber alle anderen Energien ebenfalls beteiligt sind, aber seltener vorkommen, kann man nur "verwaschene" Interferenzfiguren erwarten.

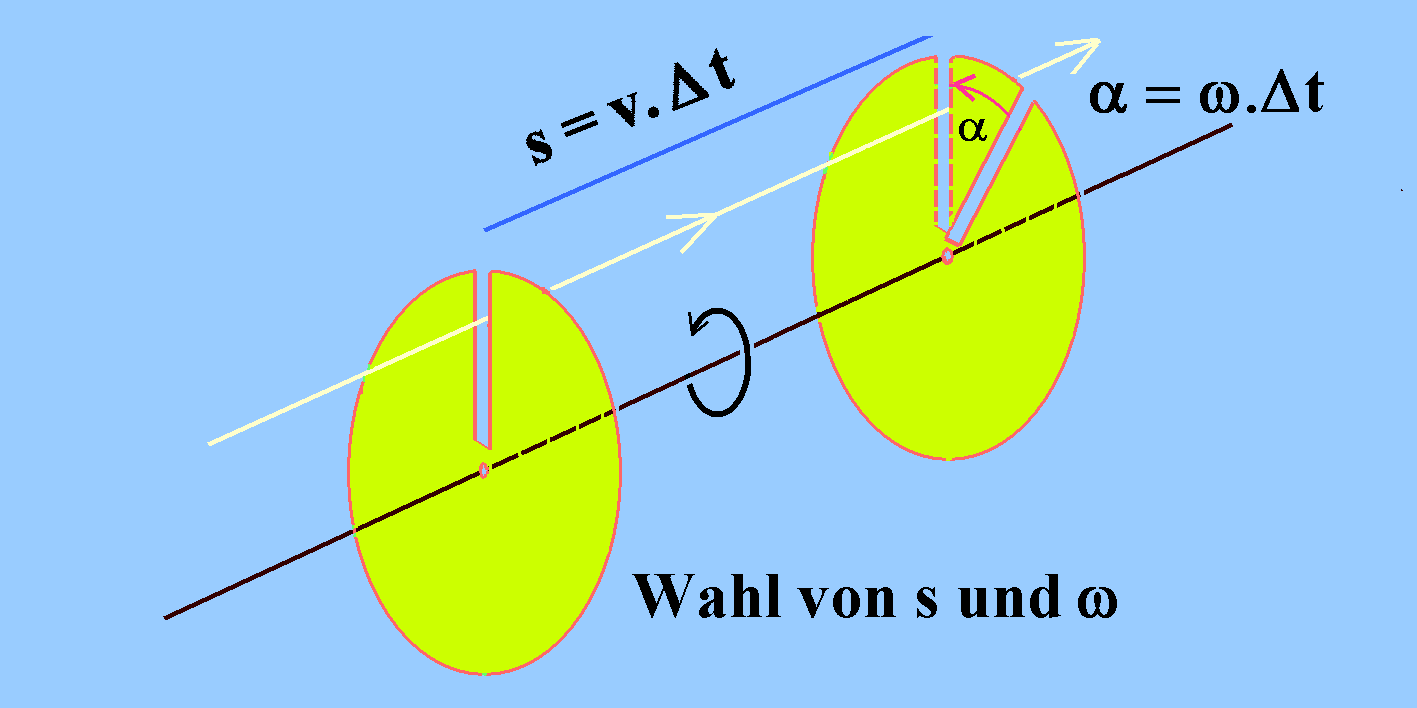  Man könnte aus dem Geschwindigkeitsspektrum durch einen Zerhacker ("Chopper") bestimmte Anteile herausschneiden. Ein Zerhacker besteht aus zwei rotierenden Scheiben auf einer gemeinsamen Achse mit einem schmalen radialen Schlitz. Bei den beiden Scheiben sind die Schlitze um einen bestimmten Winkel gegeneinander verdreht. Der erste Schlitz A erlaubt einer bestimmten Zahl von Teilchen das Passieren. Wegen unterschiedlicher Laufzeiten kommt nur ein Bruchteil von ihnen dann am Schlitz der zweiten Scheibe  B an, wenn dieser die frühere Stellung von Schlitz A erreicht hat. Nur solche Teilchen passieren.

• Ein anderes Verfahren beruht auf der Bragg-Reflexion: Man lässt Photonen, Neutronen, Atome auf einen drehbaren Einkristall fallen. Je nach Wellenlänge bzw. deBroglie-Wellenlänge (damit also je nach Geschwindigkeit) und Netzebenenabstand gibt es bestimmte Glanzwinkel, unter denen man gezielt die gewünschte Teilchensorte entnehmen kann (Bragg-Monochromator).

• Eine moderne Möglichkeit für Ionen oder Atome extrem geringer Geschwindigkeit (wenige m/s) besteht im Einsatz von (Atom- oder Ionen-) Fallen, in denen die Teilchen auf extrem geringe Temperaturen abgekühlt werden. Aus ihnen lässt man dann Teilchen "herausfallen", die nach einer bestimmten Fallstrecke eine bestimmte Fallgeschwindigkeit erreicht haben.

.

(Zeichensatz geändert 2013)