Prinzip des "Spin-Messers"
Eine Stern-Gerlach-Apparatur ("Spin-Messer") beruht grob darauf, dass das zu vermessende Elektron durch ein stark inhomogenes Magnetfeld geschickt wird. Die Stärke des Magnetfelds soll in Richtung des Magnetfelds abnehmen. Durch die Magnetfeldrichtung ist eine Bezugsrichtung ausgezeichnet.
Ein klassisches Teilchen ohne Spin (oder anderem Drehimpuls) würde unabgelenkt das Magnetfeld passieren.
Bei gleichgerichtetem Spin wird das Elektron in Magnetfeld-Richtung abgelenkt, bei entgegengesetztem Spin entgegengesetzt zum Magnetfeld.
Die jeweilige Komponente des Spins ist dann "halbzahlig", also +1/2·h/2π oder -1/2·h/2π.
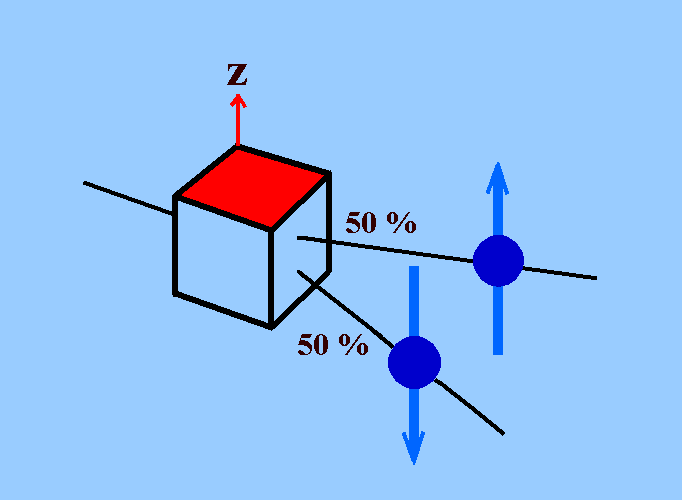
Einfache Spin-Messung
Es stellt sich heraus, dass der Spin nur in z-Richtung oder nur entgegengesetzt zur z-Richtung orientiert sein kann. Bei einer Quelle ohne Vorzugsrichtung und Spin-Messungen an vielen ihrer Elektronen ergibt die Messung in 50% aller Fälle einen Spin in z-Richtung und in 50% der Fälle einen Spin entgegengesetzt dazu.

Mehrfache Spin-Messungen
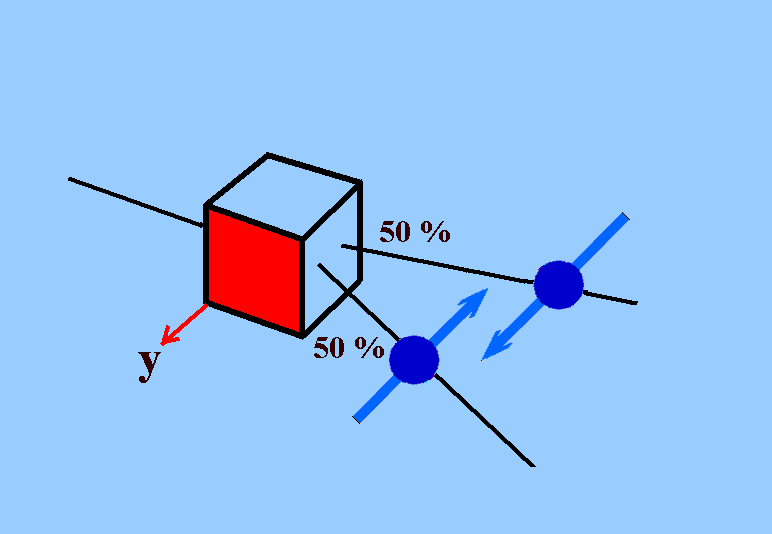
Da die y-Achse senkrecht zur z-Achse verläuft, würde man erwarten, dass kein Elektron abgelenkt wird.
Überraschenderweise ergibt die Messung auch hier in 50% aller Fälle einen Spin in y-Richtung und in 50% der Fälle einen Spin entgegengesetzt dazu. Andere Orientierung gibt es nicht.
Unter den Elektronen, die den y-Messer passieren, wird nun ein Elektron herausgegriffen, dessen Spin sich als parallel zur y-Achse gerichtet herausgestellt hat. Zuvor war der Spin doch in z-Richtung orientiert. Ist nun der Spin in z-Richtung gerichtet oder in y-Richtung?
Eine nochmalige Spin-Messung mit der z-Achse als Bezugsrichtung soll das klären.
Überraschenderweise ergibt die Messung auch hier in 50% aller Fälle einen Spin in z-Richtung und in 50% der Fälle einen Spin entgegengesetzt dazu.
Dass jetzt auch ein Spin in -z-Richtung herauskommen kann, obwohl wir von einem Elektron ausgingen, das eindeutig in +z-Richtung orientiert war, ist klassisch unverständlich.
a) Spin-Messungen bzgl. unterschiedlicher Richtungen sind nicht verträglich ("komplementär"). Jede Messung bei geänderter Bezugsrichtung macht frühere Messergebnisse ungültig. Nach einer Spin-Messung sind sämtliche Informationen über den Spin in andere Richtungen verloren gegangen.
b) Ohne eine Messung besitzt ein Elektron im Allgemeinen keinen be-stimmten Spin. Durch eine Messung wird der Spin be-stimmt bzgl. der Bezugsrichtung des Spin-Messers. Bezüglich anderer Bezugsrichtungen ist der Spin un-be-stimmt.
Stattdessen könnten wir auch sagen:
Ein Elektron besitzt nicht zugleich eine Spinkomponente in x-, y- oder z-Richtung. |
Die gleichen Ergebnisse würde man erhalten, wenn man das nach der ersten
Messung in z-Richtung orientierte Elektron noch durch einen Spin-Messer für
die x-Richtung laufen ließe.
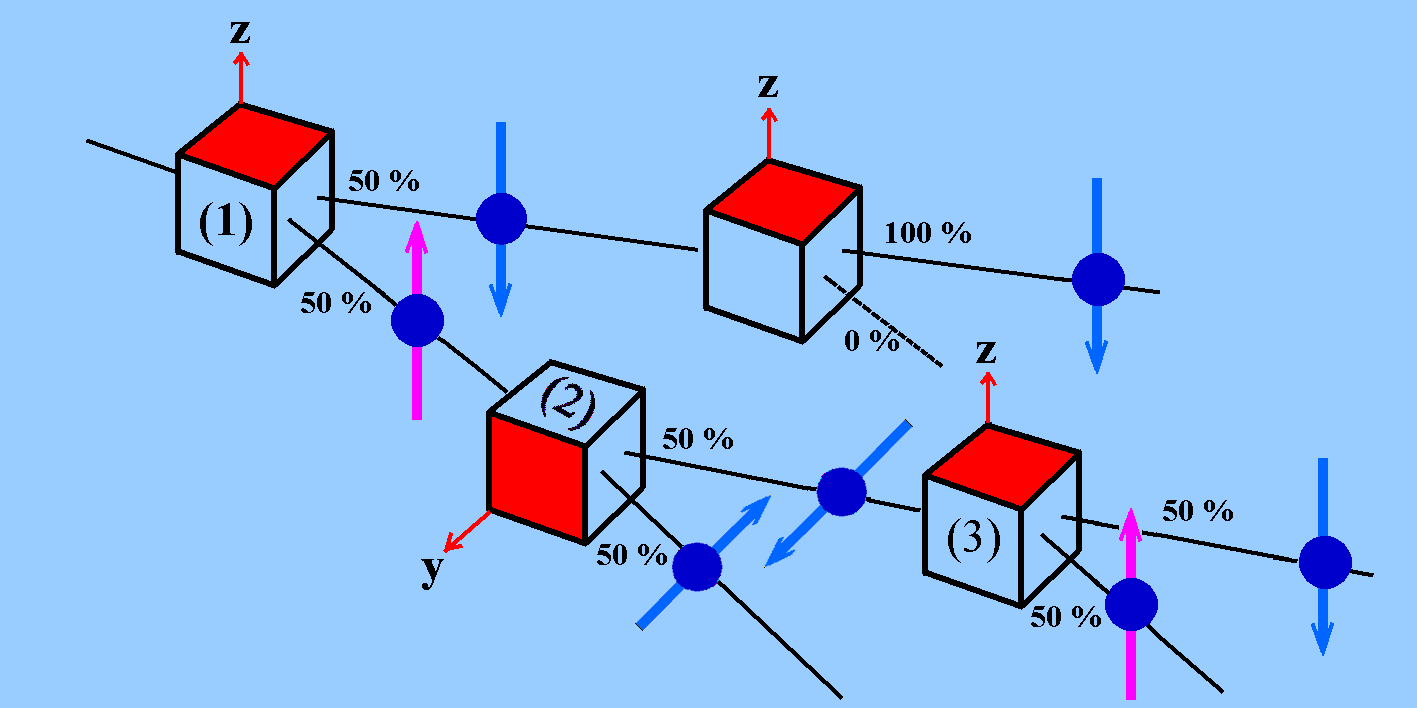 |
| (3) Zur Abbildung: Führt man unmittelbar nacheinander zwei
Spin-Messungen bzgl. der gleichen Bezugsrichtung (hier z-Richtung) durch,
dann erhält man beide Male das gleiche Ergebnis
("Messungen in der Quantenphysik sind
reproduzierbar"). Das zeigt die obere Zeile.
Führt man aber zwei Spin-Messungen bzgl. unterschiedlicher Bezugsrichtungen durch (hier erst z-Richtung, dann y-Richtung), so erhält man wieder in 50% der Fälle einen Spin in Bezugsrichtung und in 50% der Fälle einen Spin entgegen der Bezugsrichtung. Die Ergebnisse der vorausgehende Messung sind dann ungültig geworden, wie ein dritte Spin-Messung zeigt. |
Folgerung
Spin-Messungen sind das klarste Beispiel für einen Grundzug der Quantenphysik, nämlich die "Nichtexistenz aller klassisch möglichen Eigenschaften gleichzeitig" bzw. der "objektiven Un-be-stimmtheit". Messgrößen oder Eigenschaften, bei denen das der Fall ist, heißen zueinander komplementäre Messgrößen.
(Man muss allerdings sagen, dass der Spin ohnehin keine klassische Eigenschaft ist. Er ist auch in der nichtrelativistischen Quantenmechanik nicht erklärbar, sondern wird erst durch die Relativitätstheorie verständlich.)
Hier müssen wir also sagen, dass die Komponenten Sz, Sy und Sx des Elektronenspins zueinander komplementär sind. Die Spin-Komponenten haben nicht gleichzeitig be-stimmte Werte.