Binärzahlen
Binärzahlen entsprechen Schalterstellungen; eine 1 kennzeichnet einen
offenen Schalter, eine 0 einen geschlossenen Schalter ("Kurzschluss"). An
der Binärdarstellung kann man unmittelbar die Schalterstellung einer
Folge von Schaltern ablesen.
Binärzahlen entsprechen aber auch der Darstellung aller Zahlen im Computer.
In der Robotik ist eher der Zusammenhang mit den Schalterstellungen interessant;
gelegentlich kürzen wir eine Folge von Schalterstellungen durch den
dezimalen Wert der Binärzahl ab. ( 0b0110 = 6(10) ; 0b für
Binärzahl)
8-bit-Zahl = 1 Byte
| 0b.... |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 128-er |
0 64-er |
1 32-er |
0 Sechzehner |
1 Achter |
0 Vierer |
1 Zweier |
0 Einer |
| Wert: |
128 |
0 |
32 |
0 |
8 |
0 |
2 |
0 |
| Summe dezimal geschrieben:
170 |
. |
. |
. |
. |
. |
. |
. |
. |
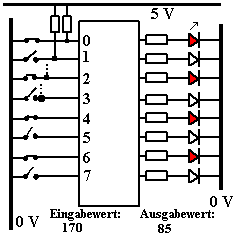 |
Alle Eingabe-Ports sind durch Pullup-Widerstände auf 5 V "hochgezogen".
Der Prozessor soll so programmiert sein, dass er für eine Invertierung
sorgt . Deshalb sind Ein- und Ausgabewerte verschieden. Sie ergänzen
sich zu 255.
Für den Eingabewert ergibt sich im Beispiel:
1.27 + 0.26 + 1.25+ 0.24 +
1.23 + 0.22 +1.21 + 0.20 = 1.128
+ 0.64 +1.32 + 0.16 + 1.8 + 0.4 + 1.2 + 0.1 = 170
und für den Ausgabewert:
0.27 + 1.26 + 0.25+ 1.24 +
0.23 + 1.22 +0.21 + 1.20 = 0.128
+ 1.64 +0.32 + 1.16 + 0.8 + 1.4 + 0.2 + 1.1 = 85 |
Größte 8-bit-Zahl : 0b11111111 = 128 + 64 + 32 + 16 + 8 + 4 +
2 + 1 = 255
Integer-Zahlen bestehen aus 2 Bytes:
In Binärzahlen-Darstellung:
| 0b |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
| Wert: |
1*32768 |
0*16384 |
1*8192 |
0*4096 |
1*2048 |
0*1024 |
512 |
0*256 |
128 |
0*64 |
32 |
0*16 |
8 |
0*4 |
2 |
0*1 |
| Summe dezimal geschrieben:
???? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Größte 2-Byte-Zahl (Integer-Zahl):
0b1111111111111111 = 32768 + 16384 + 8192 + 4096 + 2048 + 1024
+ 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 65535
Häufig wird das höchste bit als Vorzeichenbit gewählt. Dann
können mit 2 Bytes Zahlen zwischen - 32767 und + 32767 dargestellt werden.
Hexadezimal-Darstellung von Zahlen (häufig
durch 0x eingeleitet):
Statt im Zweier-System können Zahlen auch in anderen Systemen, z.B.
im 16-er System dargestellt werden. Die einzelnen Ziffern können dann
von 0 bis F = 15 gehen.
| Hex-Ziffer |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
| Ziffernwert, dezimal geschrieben: |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Die Notenstufen der Kollegstufe sind dem Hexadezimal-System perfekt angepasst.
Um gleichgeschriebene Hexadezimal- und Dezimalzahlen nicht zu verwechseln,
werden nur die Dezimalzahlen mit ihren üblichen Namen gelesen. Bei anderen
Zahlensystemen, wie dem Hexadezimal-System, werden Zahlen gelesen, indem
ihre Ziffernfolge genannt wird. 60 wird nur im Dezimalsystem "sechzig" gelesen.
Im Hexadezimal-System wird die Zahl mit "sechs-null" gelesen.
| Zahl, hexadezimal geschrieben 0x8A |
8 |
A |
| Ziffernwert |
8*16 |
10*1 |
| Zahl, dezimal geschrieben: 138 |
128 |
10 |
| Zahl, hexadezimal geschrieben 0xFF |
F |
F |
| Ziffernwert |
15*16 |
15*1 |
| Zahl, dezimal geschrieben: 255 |
240 |
15 |
Die größte 1-Byte-Zahl lautet also in den verschiedenen
Zahlensystemen: 0b11111111 = 0xFF = 255
Die größte 2-Byte-Zahl ist 0xFFFF = 65535.
Ganzzahlen = Integerzahlen
Wenn sie 2 Bytes umfassen, können sie Dezimalzahlen zwischen 0 und 65535
darstellen oder zwischen - 32767 und + 32767 . Der Zahlenbereich wird mit
zunehmender Zahl der verwendeten Bytes größer. Multipliziert man
Fließkomma-Zahlen mit einem Faktor, z.B. 1 000 000, kann man kleine
Fließkommazahlen auch durch Integerzahlen darstellen. Voraussetzung
ist allerdings, dass bei Rechenoperationen Integerzahlen etwa gleicher
Größenordnung verknüpft werden.
Gleitkomma- oder Fließkomma-Zahlen
Damit sind Zahlen gemeint, die Bruchteile von 1 enthalten, z.B. 25,3345345
. Sie werden häufig durch Dezimalbrüche oder Zehnerpotenzen
dargestellt. Besonders die Multiplikation und Division führen schnell
zu Ergebnissen ganz anderer Größenordnung. In einem solchen Fall
kann man das Rechnen mit Gleitkommazahlen nur schwer auf das Rechnen mit
Integerzahlen zurückführen.
Bei Additionen und - eingeschränkt bei - Subtraktionen dagegen bleibt
auch das Ergebnis in gleicher Größenordnung. Dann lässt sich
die Rechnung mit Gleitkommazahlen leicht auf eine Rechnung mit Integerzahlen
zurückführen. Programmiersprachen wie FORTH bieten zwar auch
Gleitkomma-Pakete, bevorzugen aber das Rechnen mit Integerzahlen.
